DuckDB -- 浮点数的压缩

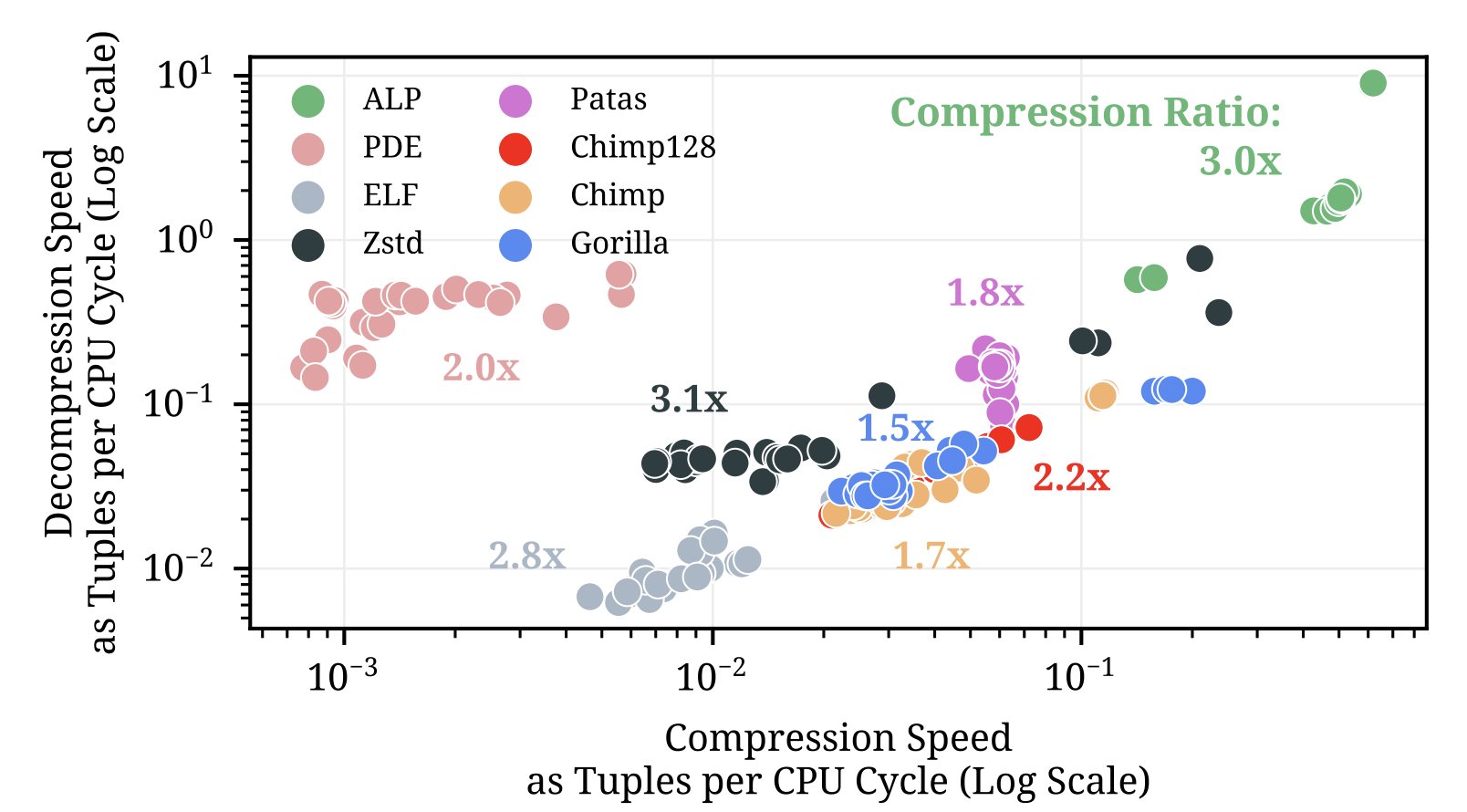
Posted at 2024-03-03 # DataBase # DuckDB # Compression # Alp

浮点数的压缩一直是一个难以解决的问题。因为其在计算机中存储格式的特殊，导致浮点数的压缩率和解压速度都不是那么令人满意。 DuckDB采用了论文 ALP 中所提出的方法来对浮点数进行压缩，各方面都取得了不错的进展，这篇博客将介绍ALP中的压缩方法。

前置知识

IEEE 754 Double 的表示方法

首先我们来回忆一下浮点数在计算机内部的表示方式。浮点数由三部分组成

符号位 (sign)
指数位 (exponent)
分数位 (fraction)

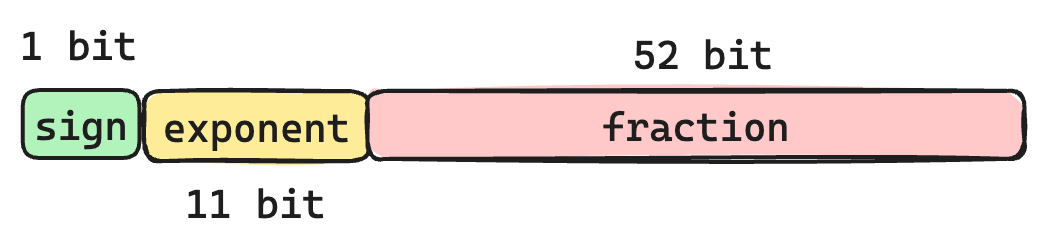
我们通过这三部分可以得到浮点数的值为

double = (-1)^{\\sign} \times 2^{(exp-1023)} \times \left(1 + \sum_{i=1}^{52}\left({b_{52-i}} {2^{-i}}\right)\right)

压缩

我们之所以难以对浮点数进行压缩，原因在于浮点数的整个二进制表示是分成三部分的，我们没有办法将其像整数一样作为一个整体进行压缩。

因此大体上对浮点数的压缩方式有

将浮点数转换为整数后进行压缩
分部份对浮点数进行进行压缩.

1. 将浮点数转化为为整数

将浮点数转化为整数的想法，看上去很简单，我们只需要乘上一个系数后，将其右边的小数部分消除即可

我们以8.0605为例, 我们仅需乘上 $10^4$ , 便可将其转化为整数, 同时我们只需要记录下这个系数, 我们便可以在解压的过程中，还原这个浮点数。

80605 = 8.0605 * 10^4 \newline 8.0605 = 80605 * 10^{(-4)}

但是这样的转换方式，因为计算机对浮点数表示的精度原因。我们没有办法在解压的时候获取于原来一样的数值，如下图所示。

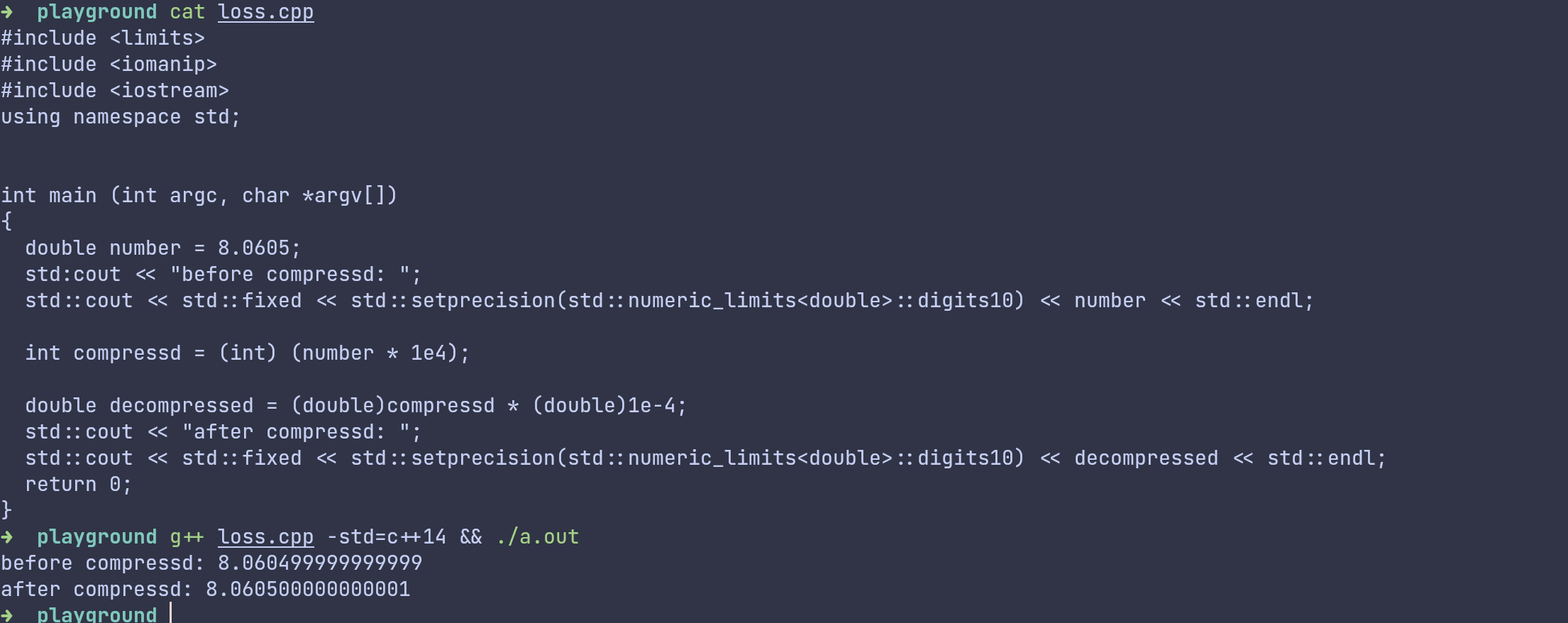
我们可以看到解压后的数据与压缩前的数据存在细微的差别，这种有损压缩对于金融相关的业务而言是不可接受的。因此我们需要找到一个方法能够对其进行无损压缩，目前最常用的方式就是增加系数。

当我们将系数增加到 $10^7$ 时，我们会发现该压缩方式变成了无损压缩。但问题也随之产生, 压缩率也下降了,在一些极端的例子中, 可能还不如不压缩。

2. 分部分进行压缩

当第一种方式无法进行有效压缩时, 我们会采取分部分进行压缩。这是因为通过观察我们发现，在一组浮点数中，指数位的方差较小，也就是指数位的值较为相似。因此我们可以对浮点数的数据集进行采样，决定一个分割点，左半部分是相似的指数位，我们对其使用dictionary encoding，而对于右半部分，我们使用bit packing进行压缩。

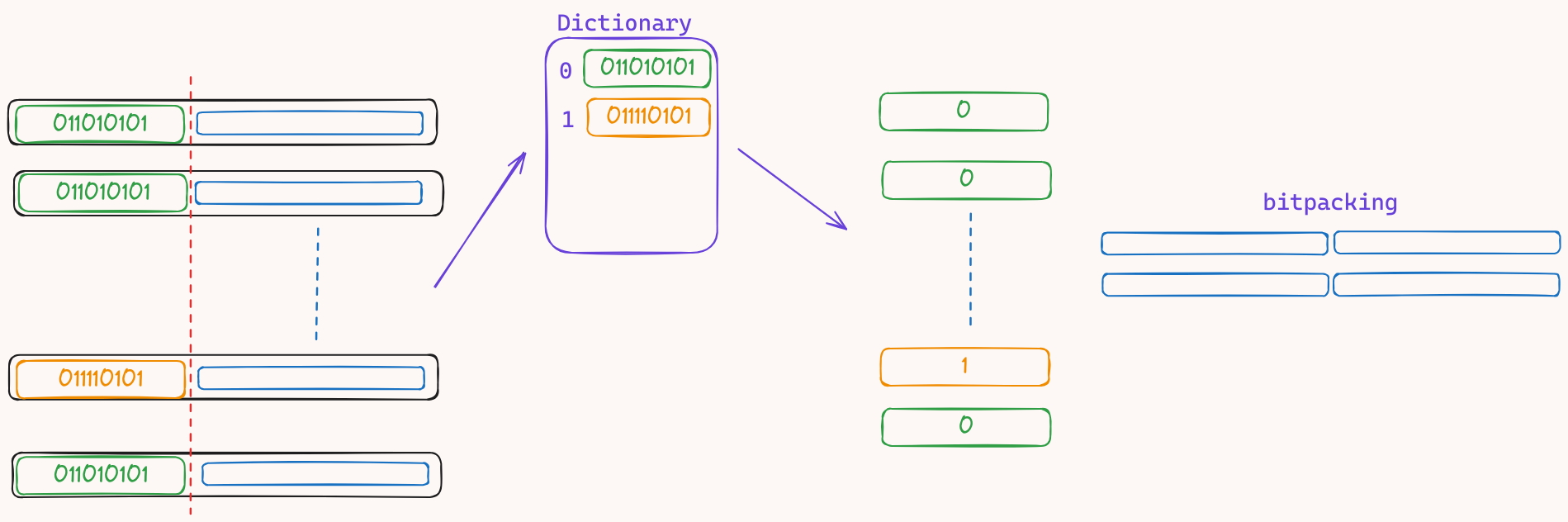
通过这种方式我们也能进行有效压缩

ALP

ALP使用的是第一种压缩方法，它首先会对待压缩的浮点数数组进行采样，确定系数 $10^e$ 。该系数确保大部分的数字可以做到无损压缩，同时它还会确定一个系数 $10^{-f}$ 。这是因为如果我们在第一步为了保证精度，选择的系数过大，那么整数后面有大量的0，同样浪费空间，因此我们选择一个合适的系数 $10^{-f}$ ,消除后置0。这里也许会有人担心再乘以一个系数可能导致引入新的误差。但是，根据论文的说法，其实并不会导致新的误差。因为论文中使用的round是自己实现的一个高效round，十分契合SIMD加速。

static const long long SWEET = (1ll << 51) + (1ll << 52);
long long fast_round(double d) {
  return static_cast<long>(d + SWEET - SWEET);
}

我们仍旧以 8.0605 为例, 假设系数分别为 $10^{14}$ , $10^{-10}$ .我们用以下的代码测试

  #include <limits>
  #include <iomanip>
  #include <iostream>
  using namespace std;
  static const long long SWEET = (1ll << 51) + (1ll << 52);
  long long fast_round(double d) {
  return static_cast<long>(d + SWEET - SWEET);
  }

  int main (int argc, char *argv[])
  {
      double number = 8.0605;
      std:cout << "before compressd: ";
      std::cout << std::fixed << std::setprecision(std::numeric_limits<double>::digits10) << number << std::endl;
      long compressd = fast_round(number * 1e14 * 1e-10);
      double decompressed = (double(compressd * 1e10) * (double)1e-14);
      std::cout << "after compressd: ";
      std::cout << std::fixed << std::setprecision(std::numeric_limits<double>::digits10) << decompressed << std::endl;
      return 0;
  }

最终的测试结果为

before compressd: 8.060499999999999

after compressd: 8.060499999999999

因此ALP的算法流程为

采样确定系数 $10^e$ , $10^{-f}$
对数组中的每一个数乘以第一步的两个系数，确定是否会损失精度

2.1. 如果不会损失精度，直接保存为整数

2.2. 如果会损失精度，作为异常值单独进行存储
对于第二步产生的整数数组使用算法FOR进行压缩

ALPRD

对于无法使用ALP的情况下(大部分数字无法无损压缩/压缩率不高)，我们会使用之前介绍的分部分压缩法。算法的流程为

对数据进行采样，确定从哪一位(P)开始分割。
P 位左边的二进制使用dictionary encode进行压缩
P 位右边的二进制使用bit packing进行压缩

总结

ALP使用非常简洁高效的算法对浮点数数组进行压缩，它不仅具有良好的压缩率，同时该算法是SIMD friendly, 可以充分利用硬件对该算法进行加速，提高解压和压缩的速度。这篇博客只是对ALP进行粗略地介绍，想要充分了解的读者还是推荐阅读论文原文ALP

tang-hi

Don't Panic