tang-hi

Don't Panic

DuckDB -- ART索引

Posted at # DataBase # DuckDB

DuckDB不同于其他的数据库，并没有使用B+树作为主要索引结构，而是使用了ART(Adaptive Radix Tree)作为它内部的主要索引结构。本文将介绍这一索引

ART(Adaptive Radix Tree)

ART 索引是由Viktor Leis, Alfons Kemper, Thomas Neumann等人提出，它相比于B+数的主要区别在于B+树是面向磁盘的，而ART则是面向内存的。即ART索引是需要全部加载到内存中的。DuckDB之所以选择这个索引有以下几方面的考虑

  1. 随着内存越来越大，并且价格也越来越便宜，我们可以使用纯内存的索引，从而避免磁盘IO，提升性能。
  2. ART索引可以很大程度上的节省空间。
  3. ART索引支持范围查询。
  4. ART索引有着较高的性能。

后续本文会先介绍ART这一数据结构，然后配合着DuckDB的代码描述ART是如何实现的。

数据结构

在讲ART索引之前，我们先看一下Trie树。(如果你不知道Trie树，可以参考Trie )

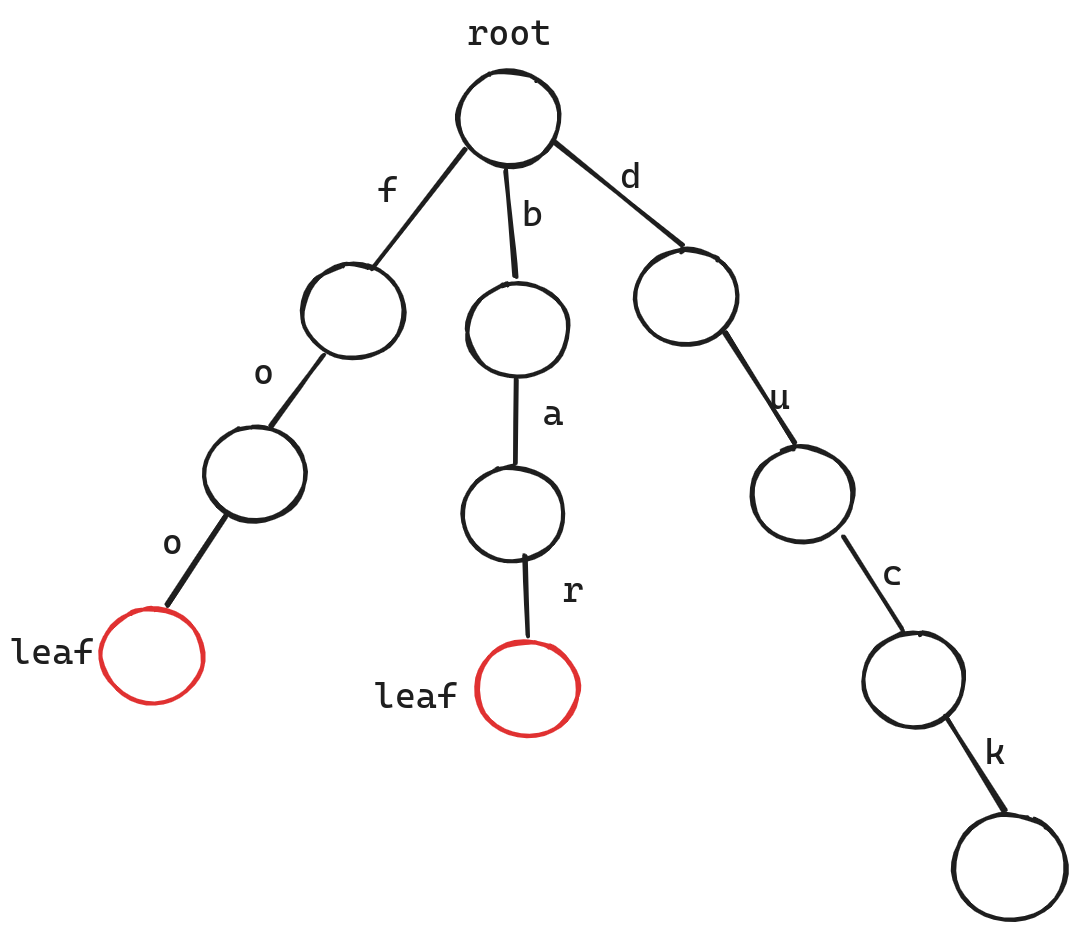
我们可以看到Trie树在检索时的优点是，它的检索时间仅与最长的字符串长度有关，而与存储的字符数量无关，这一特性在数据量极大的情况下十分优秀。但是它的缺点是浪费空间，即每个内部节点都需要保存固定数量的指针，即使它仅有极少的子结点。

比如图中的root节点，尽管他只有三个子结点，但是它仍然需要保存指向a,c,e...的空指针。这十分浪费空间。其次Trie树仅支持保存字符串。

ART则是在Trie树的基础上，解决了它缺点的同时，保留了它的优点。下面我们来介绍ART索引。

对于一个索引而言，我们希望它有以下两个特点

  1. 查询速度快
  2. 空间占用小

但是如果我们使用Trie树做索引(ART是Trie的一个变种)，我们就要面临取舍，如果内部节点可以拥有的最大子结点越多(空间占据越多)，那么它的高度也越低(速度越快)。如果内部节点拥有的最大子结点越少(空间占据越少)，那么他的高度也越高(速度越慢)。

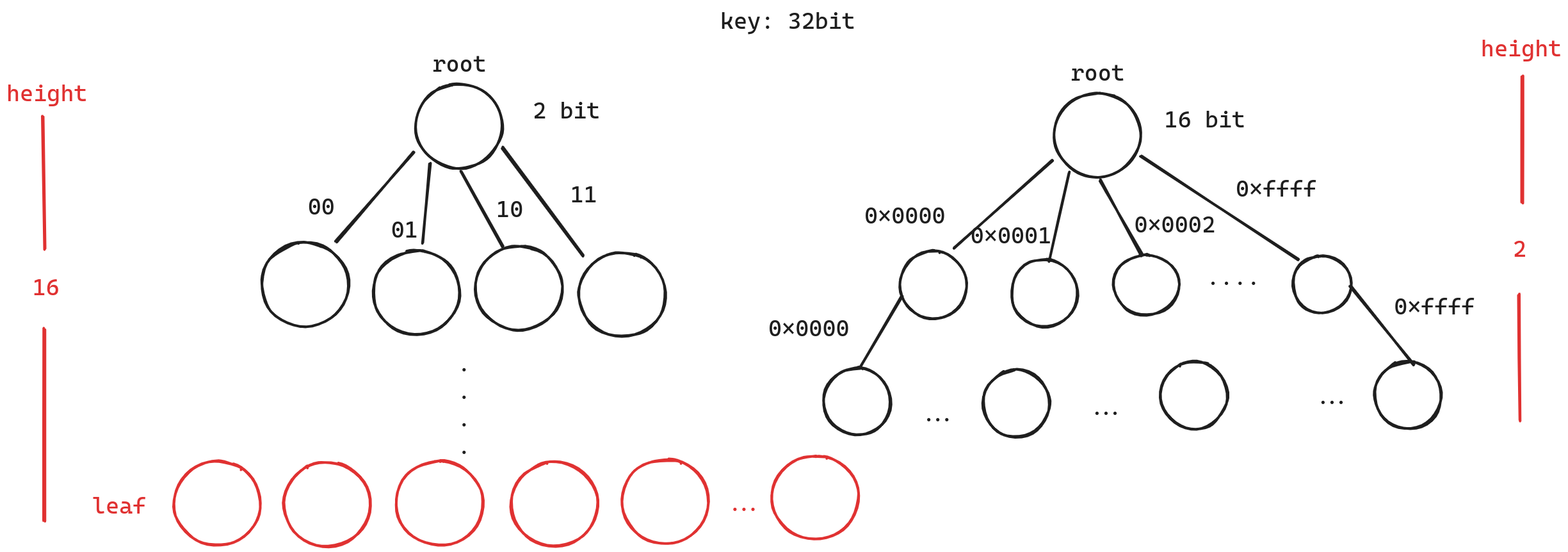
ART树选择每个内部节点的大小为8bit(子结点的数量为256),刚好是一个byte。这样的好处是免去了内存对齐的问题，同时在空间与速度上取得了一个较好的平衡。我们称内部节点所占据的位宽为span.

尽管如此，面对稀疏的数据时，每个节点有256个子结点仍旧会浪费空间，为了解决这个问题。ART将内部节点进一步细分为以下四类, 我们分别来对其进行介绍。

  1. Node4
  2. Node16
  3. Node48
  4. Node256

Node4

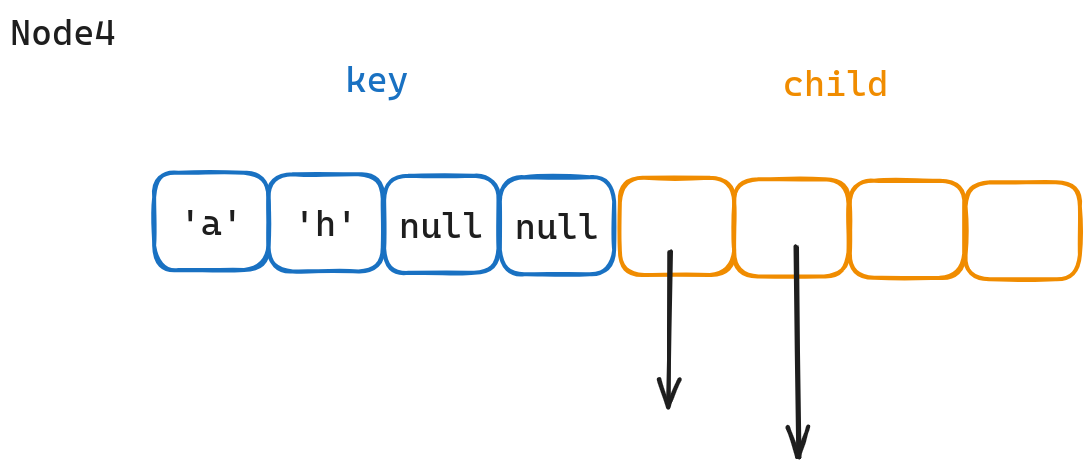
从图中可以看出，Node4分为两个部分，一个是key数组，一个是child数组。key数组存放key的部分内容(也就是key的一个byte)，child数组则是保存对应的子结点的指针。注意，我们为了可以范围查询，key数组要求顺序存储。

Node16

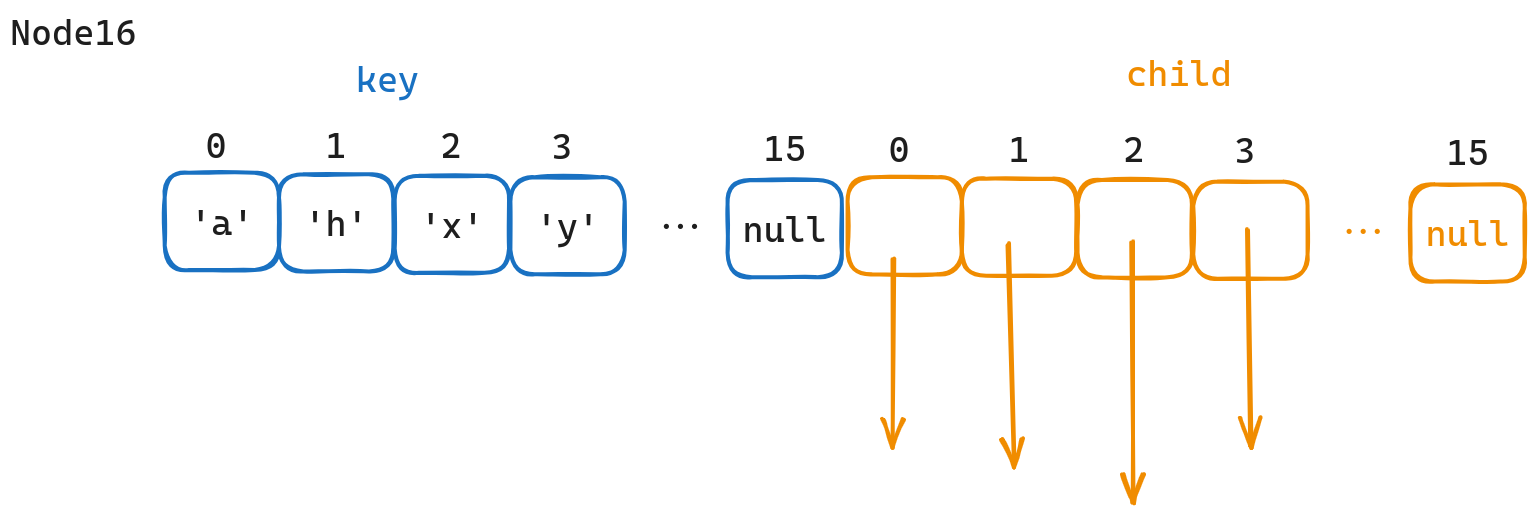
Node16和Node4几乎一样，区别只是从4个slot变为16个slot

Node48

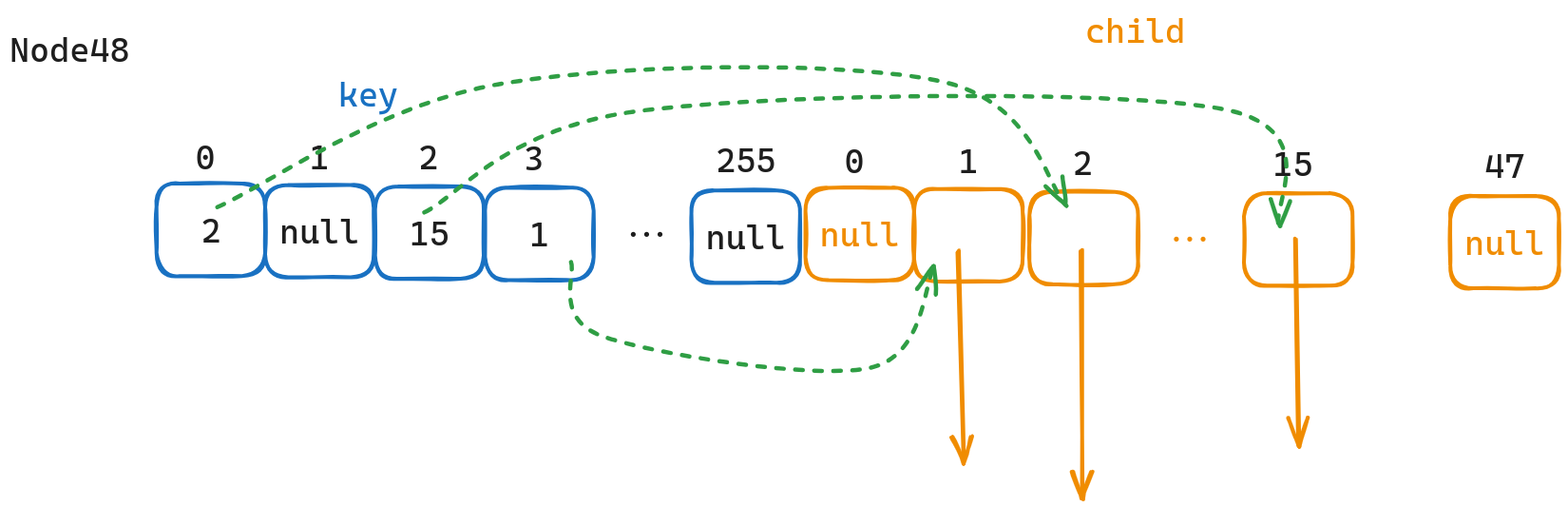
Node48和之前介绍的Node一样也是分为key数组和child数组,区别在于Node48的key数组长度为256,这样子我们就无须通过遍历找到对应的数组，而是可以直接通过key的二进制值作为下标直接定位到对应的key slot。key slot中存放的是指针，指向对应的子结点在child数组中的位置。因此child数组的长度仅需要48就可以了。

实际查询仅需要child_array[key_array[key]]即可。

Node256

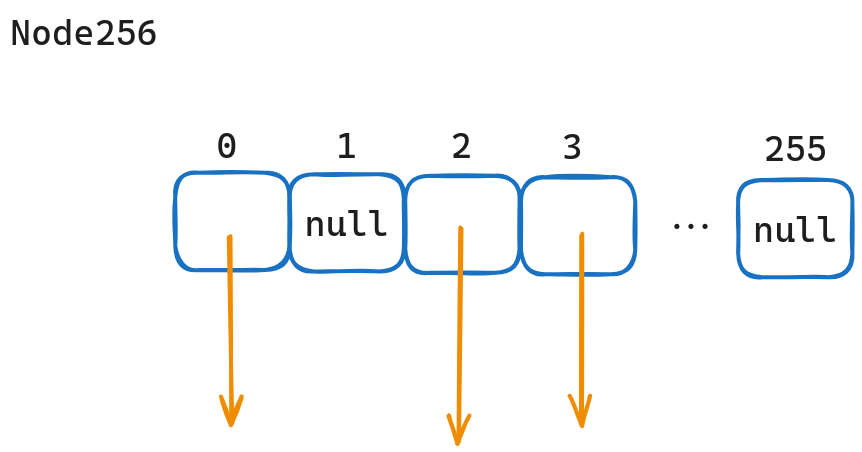
Node256就是Trie树原始的内部节点表示形式，仅需要一个数组，数组的下标即为key，数组中存放的就是子结点的指针。

各种不同类型的Node可以相互转换，如果子结点数量超过限制容量就向上转换，如果节点数量相较于限制容量太小就向下转换。

Leaf

ART中的叶节点存放的就是Key对应的Value值 ART的叶节点可以采用三种形式

  1. 单独有一个叶节点类型专门保存Value
  2. 和中间节点保持一致的类型，唯一区别则是child数组不保存指针而是值
  3. 如果值足够小可以通过位操作和指针一起保存，那么我们可以将值直接存放在内部节点中。

DuckDB采用的是第一种方式。

优化

在解决了ART的空间问题，我们希望可i进一步优化查询速度，即减少树的高度。论文中有两种方式，但实际上我们可以通过一种简单的做法同时获得这两种优化，每个节点加上Prefix标识。

  1. lazy expansion

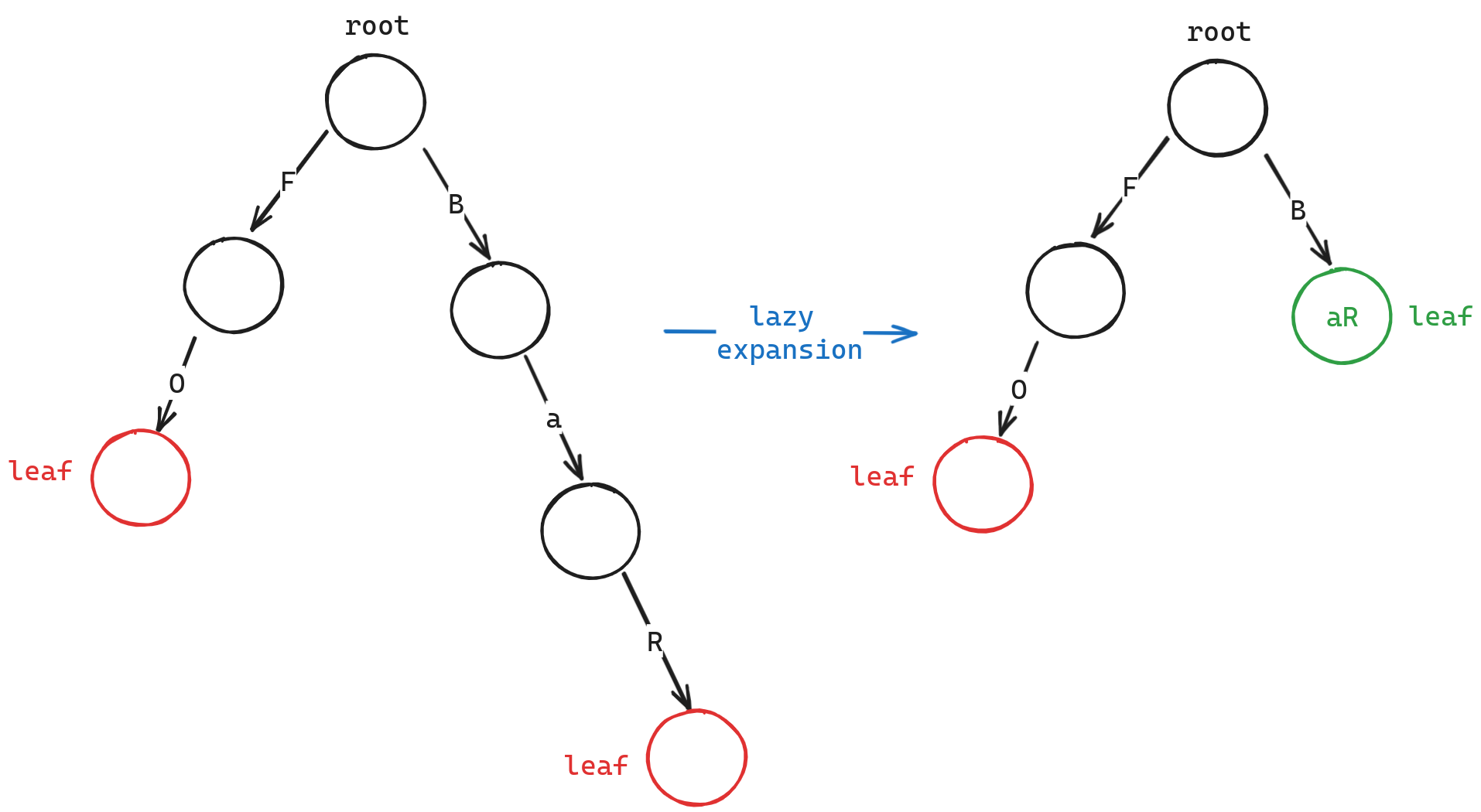
其实这个优化相当简单，我们只需Leaf可以保存多个byte即可，这样子对于多个只有一个子结点的路径来说，我们可以将其都保存在Leaf中，从而减少树的高度。

  1. path compression

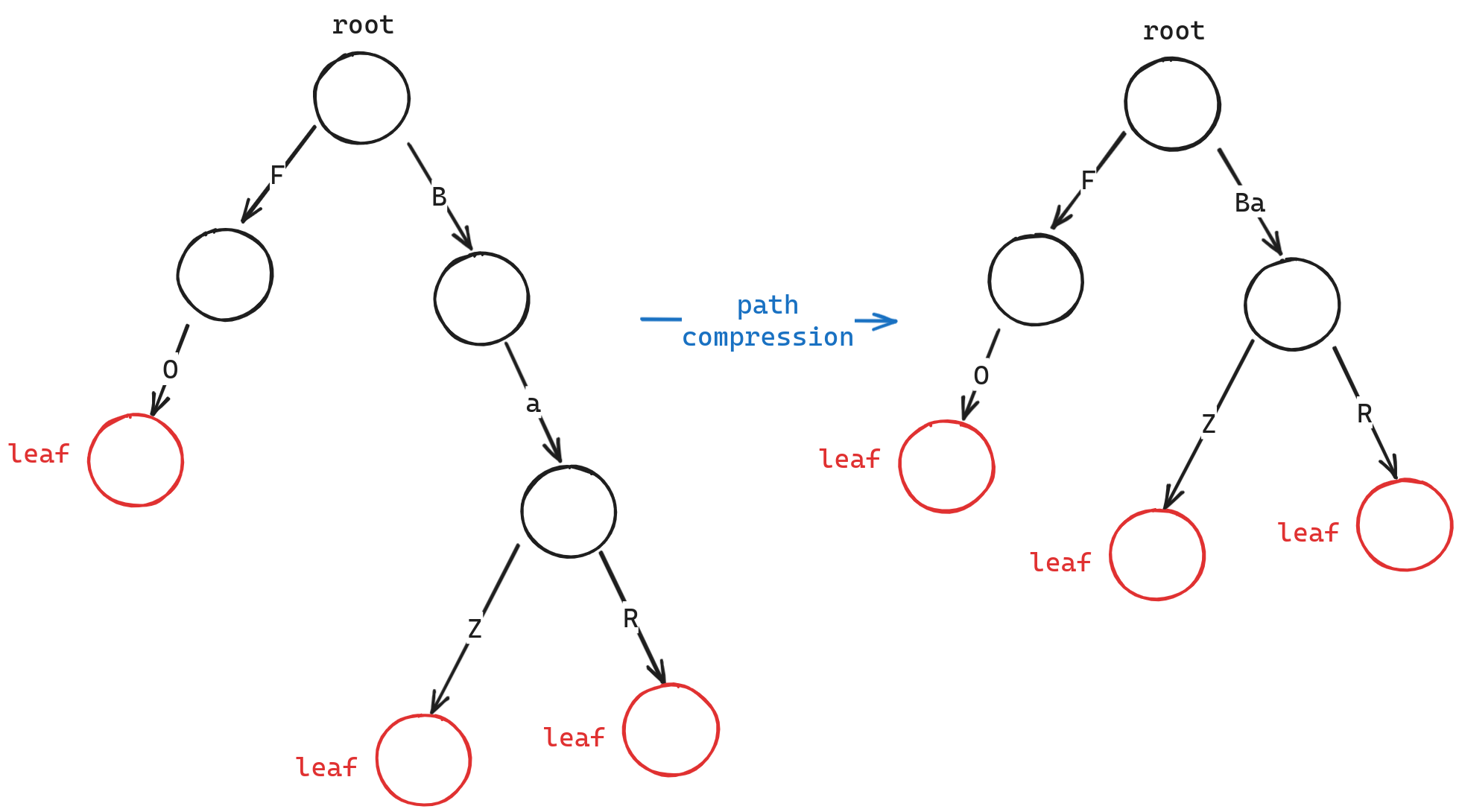
这个优化和lazy expansion类似，我们只需让内部节点可以保存多个byte即可。即如果内部节点有相同的前缀，我们可以将其保存在Prefix中，key数组仅仅只对key不同的部分作区分。这样子也可以有效的减少树的高度。

如果这里没看懂也没关系，后续我们会分析DuckDB的代码，那样会更加清晰。

数据转换

对于ART来说，我们前面介绍的都是对于字符串类型，如果作为一个被广泛使用的索引，那我们也需要支持不同类型的数据。而ART索引实际上是把Key作为数据流进行处理的，也就是说如果想要通过ART进行范围搜索，我们需要让Key保持一个性质，即二进制的大小与该类型的语义大小相同。即

memcmp(binary(x),binary(y))<0  ⟺  x<y\text{memcmp}(binary(x), binary(y)) < 0 \iff \text{x} < \text{y} memcmp(binary(x),binary(y))=0  ⟺  x=y\text{memcmp}(binary(x), binary(y)) = 0 \iff \text{x} = \text{y} memcmp(binary(x),binary(y))>0  ⟺  x>y\text{memcmp}(binary(x), binary(y)) > 0 \iff \text{x} > \text{y}

因此我们需要对某些数字进行转换

  1. unsigned integers

    无需转化，已经满足需求。

  2. signed integers

    将符号位flip即可

  3. Floating Point Numbers

    static inline uint32_t EncodeFloat(float x) {
	uint64_t buff;

	//! zero
	if (x == 0) {
		buff = 0;
		buff |= (1u << 31);
		return buff;
	}
	// nan
	if (Value::IsNan(x)) {
		return UINT_MAX;
	}
	//! infinity
	if (x > FLT_MAX) {
		return UINT_MAX - 1;
	}
	//! -infinity
	if (x < -FLT_MAX) {
		return 0;
	}
	buff = Load<uint32_t>(const_data_ptr_cast(&x));
	if ((buff & (1u << 31)) == 0) { //! +0 and positive numbers
		buff |= (1u << 31);
	} else {          //! negative numbers
		buff = ~buff; //! complement 1
	}

	return buff;
}

  4. Character Strings

    UCA算法已经做出了定义

  5. Null

    我们可以将该值设置为比最大位数仍多1位。

  6. Compound Keys

    按照其包含的基本类型进行拼接即可

源码解析

这一章节我们通过阅读DuckDB的源码，来看一下ART索引的实现。 ART索引的相关实现都在art.cpp和art.hpp，我们主要关注Insert和Find, 其他的函数留给读者自行了解。

Insert

bool ART::Insert(Node &node, const ARTKey &key, idx_t depth, const row_t &row_id) {

	if (!node.IsSet()) {
		// node is currently empty, create a leaf here with the key
		Leaf::New(*this, node, key, depth, row_id);
		return true;
	}

	if (node.DecodeARTNodeType() == NType::LEAF) {

		// add a row ID to a leaf, if they have the same key
		auto &leaf = Leaf::Get(*this, node);
		auto mismatch_position = leaf.prefix.KeyMismatchPosition(*this, key, depth);

		// identical equal
		if (mismatch_position == leaf.prefix.count && depth + leaf.prefix.count == key.len) {
			return InsertToLeaf(node, row_id);
		}

		// example:
		// prefix : hello
		// key[depth] : heel;
		// mismatch_position = 2
		// replace leaf with Node4 and store both leaves in it
		auto old_node = node;
		auto &new_n4 = Node4::New(*this, node);

		// new prefix
		// new_n4's prefix is he
		new_n4.prefix.Initialize(*this, key, depth, mismatch_position);

		// old_node's prefix change to llo
		auto key_byte = old_node.GetPrefix(*this).Reduce(*this, mismatch_position);

		// add child
		Node4::InsertChild(*this, node, key_byte, old_node);

		Node leaf_node;
		Leaf::New(*this, leaf_node, key, depth + mismatch_position + 1, row_id);
		// add child
		Node4::InsertChild(*this, node, key[depth + mismatch_position], leaf_node);

		return true;
	}

	// handle prefix of inner node
	auto &old_node_prefix = node.GetPrefix(*this);
	if (old_node_prefix.count) {

		auto mismatch_position = old_node_prefix.KeyMismatchPosition(*this, key, depth);
		if (mismatch_position != old_node_prefix.count) {

			// prefix differs, create new node
			auto old_node = node;
			auto &new_n4 = Node4::New(*this, node);
			new_n4.prefix.Initialize(*this, key, depth, mismatch_position);

			auto key_byte = old_node_prefix.Reduce(*this, mismatch_position);
			Node4::InsertChild(*this, node, key_byte, old_node);

			Node leaf_node;
			Leaf::New(*this, leaf_node, key, depth + mismatch_position + 1, row_id);
			Node4::InsertChild(*this, node, key[depth + mismatch_position], leaf_node);

			return true;
		}
		depth += node.GetPrefix(*this).count;
	}

	// recurse
	D_ASSERT(depth < key.len);
	auto child = node.GetChild(*this, key[depth]);
	if (child) {
		bool success = Insert(*child, key, depth + 1, row_id);
		node.ReplaceChild(*this, key[depth], *child);
		return success;
	}

	// insert at position
	Node leaf_node;
	Leaf::New(*this, leaf_node, key, depth + 1, row_id);
	Node::InsertChild(*this, node, key[depth], leaf_node);
	return true;
}

代码还是比较多的，我们先介绍一下参数的意义

  1. node 即为当前要进行插入的节点.

  2. key 即为要插入的key

  3. depth

    即当前已经处理到key的第几个byte,举个例子，key为hello, depth为3，那么说明he已经保存在了node的祖先节点中，我们当前要处理的是l。

  4. row_id 即为key对应的value值.

bool ART::Insert(Node &node, const ARTKey &key, idx_t depth, const row_t &row_id) {

	if (!node.IsSet()) {
		// node is currently empty, create a leaf here with the key
		Leaf::New(*this, node, key, depth, row_id);
		return true;
	}
}

如果当前节点为空，那么直接设置该节点为叶节点，并且将row_id进行保存，注意这里我们会使用lazy-expansion, 即将key剩余未处理的字符全部保存在叶节点中。

bool ART::Insert(Node &node, const ARTKey &key, idx_t depth, const row_t &row_id) {

	// .... skip
	if (node.DecodeARTNodeType() == NType::LEAF) {

		// add a row ID to a leaf, if they have the same key
		auto &leaf = Leaf::Get(*this, node);
		auto mismatch_position = leaf.prefix.KeyMismatchPosition(*this, key, depth);

		// identical equal
		if (mismatch_position == leaf.prefix.count && depth + leaf.prefix.count == key.len) {
			return InsertToLeaf(node, row_id);
		}

		// example:
		// prefix : hello
		// key[depth] : heel;
		// mismatch_position = 2
		// replace leaf with Node4 and store both leaves in it
		auto old_node = node;
		auto &new_n4 = Node4::New(*this, node);

		// new prefix
		// new_n4's prefix is he
		new_n4.prefix.Initialize(*this, key, depth, mismatch_position);

		// old_node's prefix change to llo
		auto key_byte = old_node.GetPrefix(*this).Reduce(*this, mismatch_position);

		// add child
		Node4::InsertChild(*this, node, key_byte, old_node);

		Node leaf_node;
		Leaf::New(*this, leaf_node, key, depth + mismatch_position + 1, row_id);
		// add child
		Node4::InsertChild(*this, node, key[depth + mismatch_position], leaf_node);

		return true;
	}
	
	//skip....
}

如果当前遇到的是叶节点，同时key完全相同，那么我们可以直接将row_id插入叶节点中。不然的话，我们需要将叶节点变为内部节点，同时将不同的部分作为该内部节点的叶节点。如下图所示。

bool ART::Insert(Node &node, const ARTKey &key, idx_t depth, const row_t &row_id) {

	// skip ....
	// handle prefix of inner node
	auto &old_node_prefix = node.GetPrefix(*this);
	if (old_node_prefix.count) {

		auto mismatch_position = old_node_prefix.KeyMismatchPosition(*this, key, depth);
		if (mismatch_position != old_node_prefix.count) {

			// prefix differs, create new node
			auto old_node = node;
			auto &new_n4 = Node4::New(*this, node);
			new_n4.prefix.Initialize(*this, key, depth, mismatch_position);

			auto key_byte = old_node_prefix.Reduce(*this, mismatch_position);
			Node4::InsertChild(*this, node, key_byte, old_node);

			Node leaf_node;
			Leaf::New(*this, leaf_node, key, depth + mismatch_position + 1, row_id);
			Node4::InsertChild(*this, node, key[depth + mismatch_position], leaf_node);

			return true;
		}
		depth += node.GetPrefix(*this).count;
	}

	// recurse
	D_ASSERT(depth < key.len);
	auto child = node.GetChild(*this, key[depth]);
	if (child) {
		bool success = Insert(*child, key, depth + 1, row_id);
		node.ReplaceChild(*this, key[depth], *child);
		return success;
	}

	// insert at position
	Node leaf_node;
	Leaf::New(*this, leaf_node, key, depth + 1, row_id);
	Node::InsertChild(*this, node, key[depth], leaf_node);
	return true;
}

如果是内部节点，那我们需要讨论

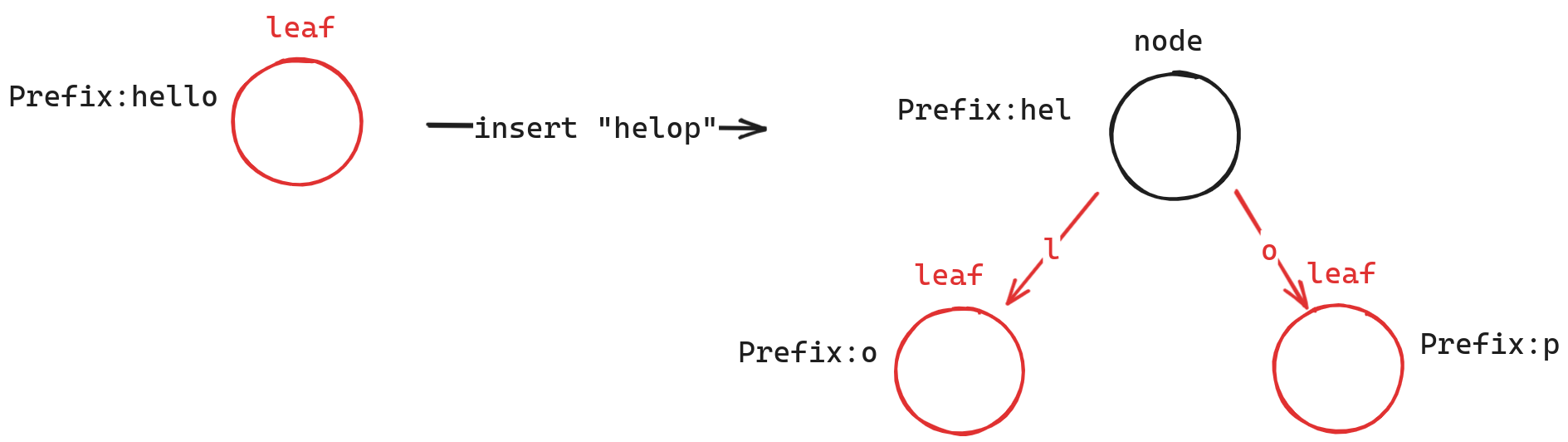
  1. 如果前缀完全相同，即“hello”和”hellopxxx“。那么我们仅需要找出子结点进行插入即可。如下图所示。
  1. 如果前缀有不同指出，那么我们需要创建一个新的节点。并将两个节点作为子结点进行插入。如下图所示。

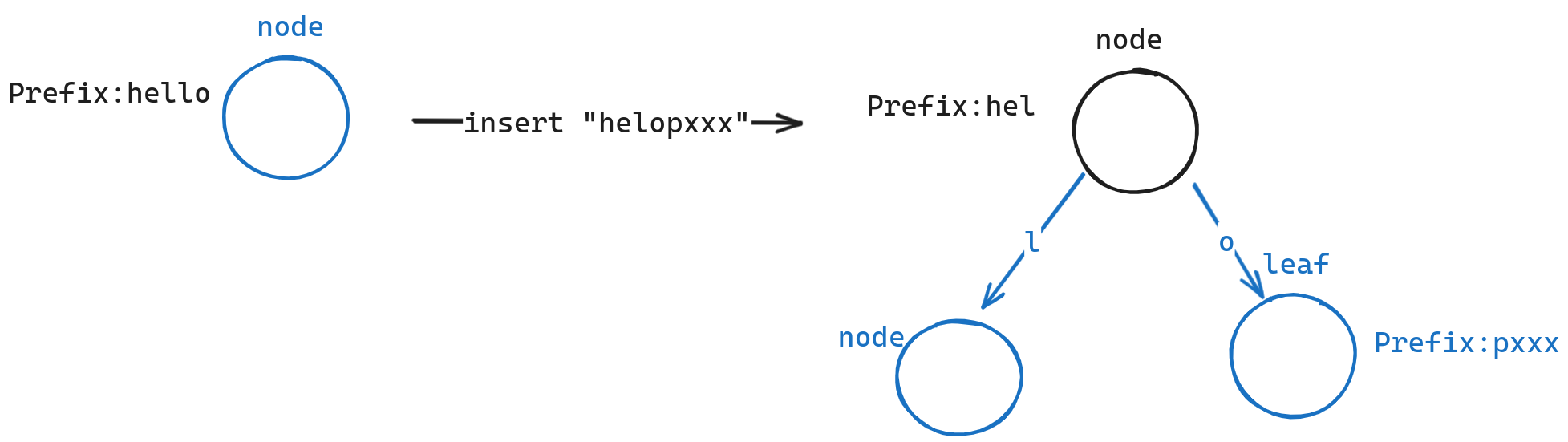
可以看到，我们只需要在内部节点，和叶节点中支持存储多个字符后，便天然支持上述的有化方案。

Find

Node ART::Lookup(Node node, const ARTKey &key, idx_t depth) {

	while (node.IsSet()) {
		if (node.DecodeARTNodeType() == NType::LEAF) {
			auto &leaf = Leaf::Get(*this, node);

			// check if leaf contains key
			for (idx_t i = 0; i < leaf.prefix.count; i++) {
				if (leaf.prefix.GetByte(*this, i) != key[i + depth]) {
					return Node();
				}
			}
			return node;
		}
		auto &node_prefix = node.GetPrefix(*this);
		if (node_prefix.count) {
			for (idx_t pos = 0; pos < node_prefix.count; pos++) {
				if (key[depth + pos] != node_prefix.GetByte(*this, pos)) {
					// prefix mismatch, subtree of node does not contain key
					return Node();
				}
			}
			depth += node_prefix.count;
		}

		// prefix matches key, but no child at byte, does not contain key
		auto child = node.GetChild(*this, key[depth]);
		if (!child) {
			return Node();
		}

		// recurse into child
		node = *child;
		D_ASSERT(node.IsSet());
		depth++;
	}

	return Node();
}

查找的代码相对来说比较简单

  1. 查找到了 Leaf 节点,检查Prefix是否匹配。如果不匹配说明Key不存在，若匹配直接返回该叶节点即可。
  2. 查找到了 内部节点,检查Prefix是否匹配。如果不匹配说明Key不存在，若匹配继续搜索对应的子节点。

Last

本文介绍了DuckDB的ART索引，可以看到尽管ART索引的树会比B+树更高，因此如果是面向磁盘的情况下，B+树会比ART索引优势更大，但是如果是内存索引的情况下，ART索引更加紧凑，同时他的渐进时间复杂度仅与key的长度有关，可能也更加cache friendly？它的节点相较于B+树更加的小，可以更多的保存在cache中。从论文中的实验来看，它的性能会比B+树更好。相较于Hash table,它支持范围查询。基于此DuckDB将ART索引作为其的主要索引。