当用户在进行检索时，他往往希望搜索引擎可以迅速返回他最需要的文档信息。在这个使用场景中，我们需要解决两个问题。

1. 在确定Query的情况下，如何定量的给文档进行打分？
2. 如何在上亿乃至上百亿的文档中快速的找到与用户Query最相关的文档？

下面我们会从这两个问题出发，描述基于文本检索的搜索引擎是如何处理这两个问题(本文只做基础知识的介绍)。

从头开始发明TF-IDF和BM25

大多数人看到BM25的公式后，会选择放弃理解公式的含义，随后将其作为一个黑盒模型使用。这是因为这个公式考虑了多方面的因素，使得人们难以 一下子理解它的含义。 为了方便读者理解该公式, 我们通过再次”发明”的方式来理解这两个公式。

TF-IDF

在给定Query的情况下，我们如何衡量一篇文档比另一篇文档更加相关呢？

一个显而易见的做法是，对给定的term，我们统计文档中该term出现的次数。 出现的次数越多，那这篇文档的相关性越高。

那我们如何衡量Query与文档的相关性呢？我们可以将Query中每个term的相关性加起来，即

单独使用term出现次数来衡量文档的相关性，有两个很明显的问题

1. 对于Query中的每个term都是平等对待的，没有考虑哪些term更加重要。 例如当Query是”猫和老鼠”，检索出来的文档中很有可能是 “和” 出现次数最多的文档，这显然不是我们想要的。
2. 文档所包含的term越多，它的相关性高的可能性就越大，这显然是不合理的。 例如你的Query是”猫和老鼠”，你可能搜出来一个完全无关的文档，仅仅因为这个文档很长，而它又包含了大量”猫”和”老鼠”。

为了解决第一个问题，我们需要给予Query中的term一个权重，而term的权重应该与它在整个文档集合中的稀缺性成正比。 如果一个term在很多文档中都出现，说明它是一个常用词，比如”这”, “那”。 反之，如果一个term很少在文档中出现，说明它在文档集合中的稀缺性很高， 那么它在整个Query中的权重就应该更高。

我们如何衡量一个term在整个文档集合中的稀缺性呢？我们可以用包含这个term的文档倒数来衡量，即

为了便于后续处理，我们可以将$\text{importance}(t)$ 乘以文档总数进行归一化，即

至此，我们”发明”了IDF(Inverse Document Frequency)的概念。

那我们如何将IDF和TF结合起来呢？我们可以简单将两者相乘，即

至此，TF-IDF的基本概念基本就讲完了。但我们还需要对上述公式进行一些调整，以便更好的适应实际场景。 具体调整方式为对IDF取log。公式如下

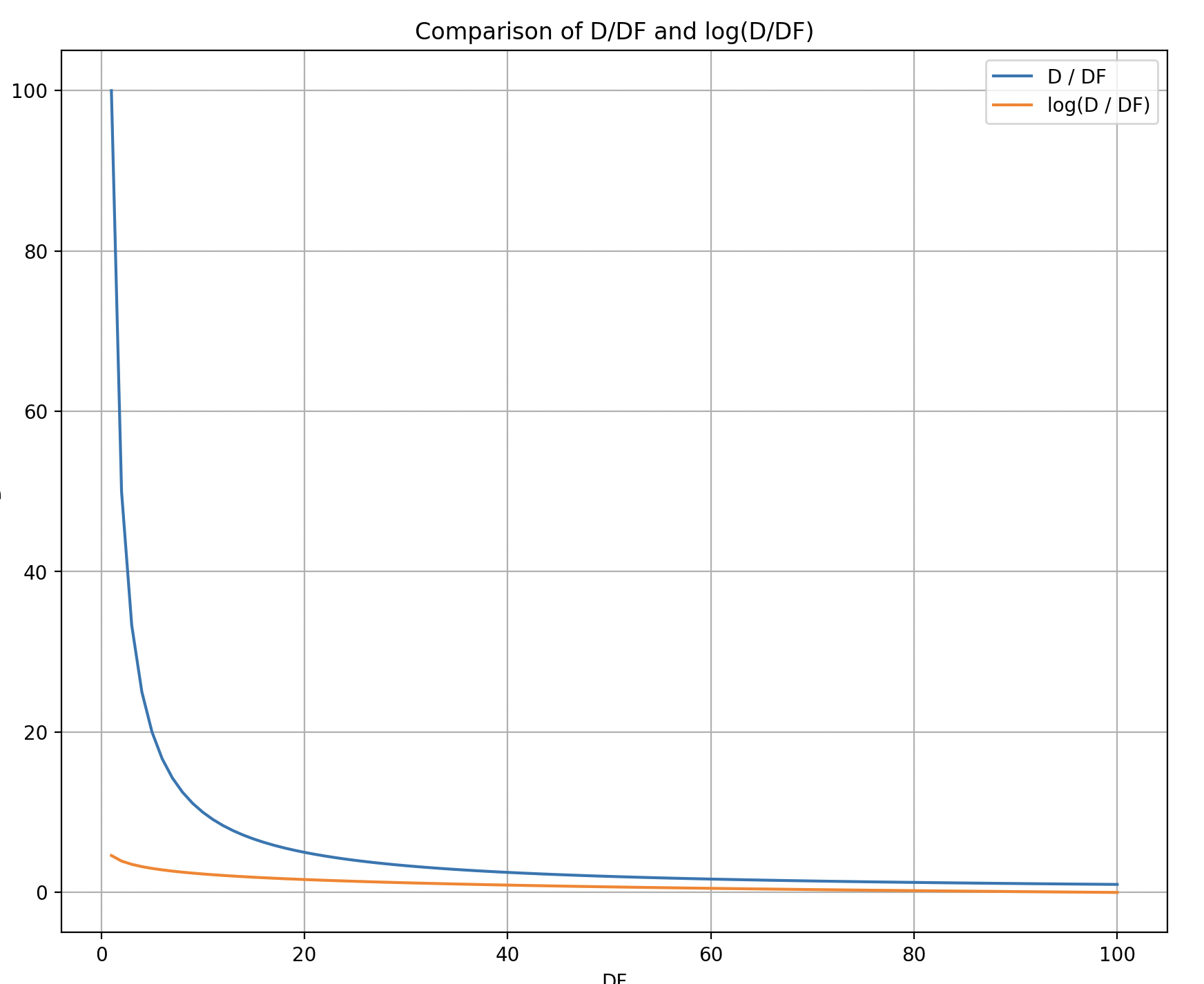
为什么要取log呢？ 我们可以从下图中看到，当DF较小时，DF轻微的变化会导致IDF剧烈变化，这显然是不合理的。

例如，当DF从1变到2时，IDF的数值减少了一半，这显然是不符合常识的， 在一个较大的文档集合中，term在两个文档中出现和在一个文档中出现, 这两者的重要性应该是差不多的。但我们的IDF公式并没有考虑这一点， 因此我们需要取log使得IDF的变化更加平滑。

BM25

在TF-IDF这一节中，我们介绍了它的两个缺点，即会偏向长文档，以及对Query中的term没有进行加权的处理。 我们已经解决了Query中term的权重问题，那么如何解决文档长度的问题呢？

文档长度的问题

检索过程中，当两篇文档的term出现的次数相同时，我们应该更加青睐于较短的文档。 因此我们需要一个公式来对文档的长度进行惩罚。

在得到这个公式之前，我们先量化一下文档的长度：用文档中term的个数来量化文档的长度，即

但是这个公式只考虑了文档的长度，而没有考虑整个文档集合。因此我们需要把文档的长度与整个文档集合的平均长度进行比较，从而评估在文档集合中，这个文档的长度是长还是短。即

在得到可以量化文档长度的公式之后，我们先暂缓一下，思考一下TF-IDF的其他问题。

Refine TF

在TF-IDF中，我们假设TF和相关性是成正比的，即TF越大，相关性越高。但这显然是不合理的。

例如，猫在一篇文档中出现了1000次，这并不意味该文档的相关性比猫只出现了100次的文档高10倍。恰恰相反, 在实际搜索中，我们会倾向于认为，当term在文档中出现的次数较多时，它相关性的边际效益会递减。

同时如果仅使用TF来衡量文档的相关性，那么对于Query: “猫和老鼠”，出现了”猫”和”老鼠”各一次的文档与出现了”猫”2次的文档的相关性是一样的， 这显然也是不合理的。

因此，我们需要对TF进行调整，使得TF较小时，相关性的增长较快，而TF较大时，相关性的增长较慢。并对于Query中的term命中数相同，不同的term越多，相关性越高。 新的TF公式如下

从图中我们可以看到，当我们加上K之后，TF的增长速度会随着TF的增加而放缓。

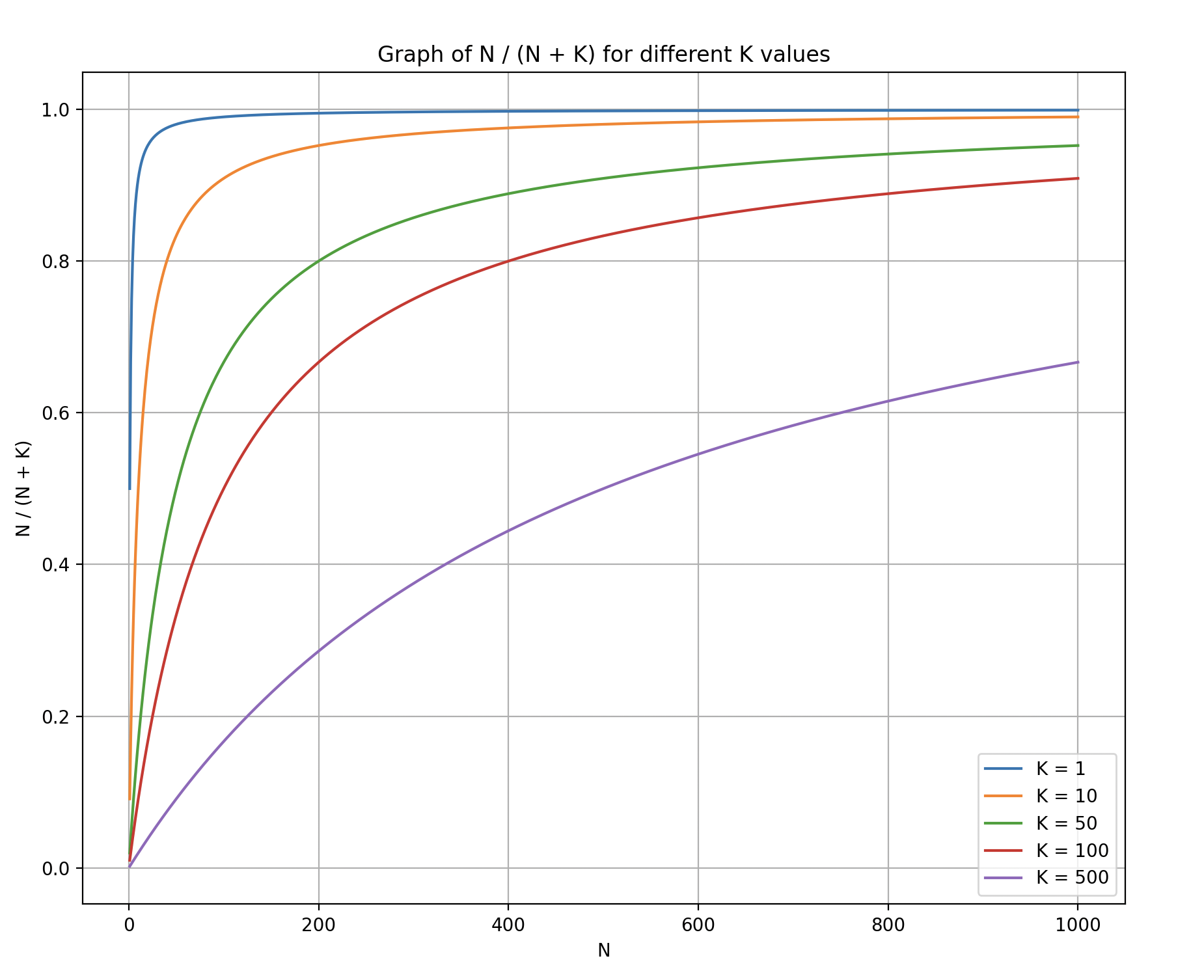
同时如果Query为”猫和老鼠”，那么出现了”猫”和”老鼠”各一次的文档, 它的相关性为 $\frac{1}{2} + \frac{1}{2} = 1$ (假设K=1)， 而出现了”猫”2次的文档，它的相关性为 $\frac{2}{3} < 1$，

到了这里还记得，我们上一节暂缓的文档长度问题吗？我们可以将文档长度的问题与TF的问题结合起来， 即将我们在上一节得到的量化文档长度的公式与新的TF公式结合起来，即

为什么这个公式是合理的呢？如果文档的长度等于平均长度，那么这个公式就等价于我们上一节得到的新的TF公式。 而当文档的长度远大于平均长度时，这个公式会增大K值，从而减小相关性，即对文档的长度进行了惩罚。而当文档的长度远小于平均长度时，这个公式会减小K值，从而增大相关性，即对文档的长度进行了奖励。

自定义文档长度的惩罚

在实际检索的场景中，我们并不总是希望文档的长度越短越好，有时候我们希望文档的长度越长越好。例如在搜索引擎中，我们希望返回的文档尽可能的丰富，这时我们可以自定义一个参数b，来调整文档长度的惩罚。即

当b=1时，公式如下所示，与之前的公式等价

当b=0时，文档的长度不再对相关性产生影响。

因此用户可以通过调整b的值来调整文档长度对相关性的影响。至此将我们的公式整合一下，即

Refine IDF

BM25中定义的IDF与我们之前定义的IDF有所不同，具体的公式如下

这是数学家出于理论上的考虑，对IDF进行了一些调整，使得IDF的变化更加平滑，同时避免了一些极端情况的发生。但是在实际情况中，Lucene对IDF进行了一些调整，具体的公式如下

即我们之前定义的IDF公式。

Warp up

将我们之前定义的TF，IDF，文档长度的惩罚，文档长度的奖励整合起来，即

我们可以发现，一个简单的BM25的公式，通过巧妙的数学，成为了文档相关性打分的事实标准。即使在深度学习的时代，BM25仍然是搜索引擎中最常用的打分公式之一。

快速求解TopK

在实际的搜索引擎中, 我们最常处理的Query就是TopK，即给定一个Query，我们需要返回与Query最相关的K个文档。

但是在几十上百亿的文档中，如何快速的找到与Query最相关的K个文档呢？我们当然可以对所有被召回的文档进行打分，然后排序，取TopK。

但是这样的延迟显然是不可接受的。因此我们需要一些技巧来加速这个过程。 这一章会介绍当前最常用的几种技术(无损检索，即检索的TopK文档是准确的)。

我们主要关注OR Query， 即Query中的term之间是或的关系。 AND Query 因为求交的特性，往往计算要求不高

DAAT(Document At A Time)

DAAT是一种朴素的方法，我们会使用一个堆用来维护当前的TopK文档。 它的特点是，对每一篇文档，我们都会计算它的得分，然后与堆顶的文档比较，如果新文档得分更高，那我们就更新堆顶的文档。

具体步骤如下

1. 对Query中每一个term，我们检索出该term对应的倒排拉链
2. 我们将这些倒排链表合并，得到一个包含所有文档ID的列表
3. 对每一个文档，我们计算它的得分，然后与堆顶的文档进行比较，如果得分更高，那么我们将堆顶的文档替换为当前文档。

我们通过如下的伪代码来描述这个过程

def DAAT(Query, document_collection):
  """
  Performs Document-At-A-Time (DAAT) retrieval.

  Args:
    Query: A list of Query terms (strings).
    document_collection: collection of documents to be searched.

  Returns:
    A list of (documentID, score) tuples, ranked in descending order of score.
  """

  inverted_index = document_collection.get_inverted_index()
  postings_lists = [inverted_index[term] for term in Query]

  merged_postings = merge_postings_lists(postings_lists)
  for doc_id in merged_postings:
    score = compute_score(Query, doc_id, document_collection)
    # Update the heap with the new score.
    if len(heap) < k:
      heapq.heappush(heap, (score, doc_id))
    elif score > heap[0][0]:
      heapq.heappushpop(heap, (score, doc_id))

TAAT(Term At A Time)

TAAT 与 DAAT一样，也是一种朴素的方法。它的特点是，我们不会像DAAT一样，使用堆来维护TopK文档，而是会遍历每一个倒排链，计算出文档的部分得分(partial score)。 同时内存中维护每一篇文档的部分得分，当我们遍历完所有的倒排链之后，我们再对文档按照得分进行排序，取TopK。它的具体步骤如下

1. 对Query中的每一个term，我们检索出该term对应的倒排链表
2. 对每一个倒排链表，我们遍历其中的每一篇文档，计算它的部分得分
3. 对每一个文档，我们将它的部分得分加到它的总得分上
4. 对所有的文档，将其按照得分进行排序，取TopK

我们通过如下的伪代码来描述这个过程

def TAAT(Query, document_collection):
  """
  Performs Term-At-A-Time (TAAT) retrieval.

  Args:
    Query: A list of Query terms (strings).
    document_collection: collection of documents to be searched.

  Returns:
    A list of (documentID, score) tuples, ranked in descending order of score.
  """

  inverted_index = document_collection.get_inverted_index()
  postings_lists = [inverted_index[term] for term in Query]

  scores = {}
  for postings_list in postings_lists:
    for doc_id in postings_list:
      score = compute_score(Query, doc_id, document_collection)
      scores[doc_id] += score

  top_k = sorted(scores.items(), key=lambda x: x[1], reverse=True)[:k]
  return top_k

Compare DAAT and TAAT

在介绍完最简单的两个朴素方法之后，我们来比较一下两种方法的优缺点。 在实际检索的场景下，我们往往会使用DAAT，不仅因为它的延迟更低，而且它的内存占用也更低。TAAT的优势在于， 他对倒排链的顺序读取，有利于CPU的cache命中以及磁盘的预读取。 但是随着文档集合的增大，TAAT的内存占用会迅速增加，而他顺序读取的优势也会因为更新文档的得分而减弱。 相反DAAT的内存占用是固定的，且在大规模文档集合中，它的延迟会比TAAT更低。因此在实际的搜索引擎中，我们往往会使用DAAT。

WAND(Weak AND)

WAND是一种基于DAAT的优化方法，它的特点是，我们会使用一个阈值来剪枝，当文档的得分低于阈值时，我们就不再计算它的得分。

他的具体步骤如下:

索引构建阶段：

1. 在索引构建阶段，我们会记录每一个term所能得到的最高得分(upper bound)，即

   $\text{upperbound}(t) = max(\text{score}(t, \forall d \in D))$

索引检索阶段:

1. 对Query中的每一个term，我们检索出该term对应的倒排链表,设置阈值为0
2. 我们将倒排链表按照Doc ID进行排序
3. 我们按顺序遍历每一个倒排链表，将term对应的upperbound进行累加，直到得分超过当前维护的阈值。
   1. 如果遍历完了所有的倒排链表，得分仍然没有超过阈值，那么检索结束，返回结果
   2. 如果得分超过了阈值，那么我们获取这条倒排链的Doc ID
      1. 如果这个Doc ID ≤ 当前记录的Doc ID，那么我们任意选择一个之前的倒排链，调用next(docid)方法, 跳转到步骤1
      2. 检查第一条倒排链的Doc ID是否等于当前记录的Doc ID，如果是，那么我们就找到了一个文档，我们计算它的得分，然后与堆顶的文档进行比较，如果得分更高，那么我们就将堆顶的文档替换为当前文档。
      3. 如果第一条倒排链的Doc ID不等于当前记录的Doc ID，那么我们任意选择一个之前的倒排链，调用next(docid)方法, 跳转到步骤1

我们通过如下的伪代码来描述这个过程

def find_pivot_term(term, threshold, postings_lists):
  """
  Find the pivot term for WAND retrieval.

  Args:
    term: A Query term (string).
    threshold: The threshold score.

  Returns:
    A tuple (posting_idx, term) of the pivot term.
  """
  score = 0
  for i, postings_list in enumerate(postings_lists):
    term = postings_list.term
    score += term.upperbound
    if score > threshold:
      return i, term

def WAND(Query, document_collection):
  """
  Performs Weak AND (WAND) retrieval.

  Args:
    Query: A list of Query terms (strings).
    document_collection: collection of documents to be searched.

  Returns:
    A list of (documentID, score) tuples, ranked in descending order of score.
  """

  inverted_index = document_collection.get_inverted_index()
  postings_lists = [inverted_index[term] for term in `Query`]
  top_k = []
  threshold = 0
  current_doc_id = None
  while True:
    sort(postings_lists, key=lambda x: x.current_doc_id())
    pivot_idx, pivot_term = find_pivot_term(postings_lists, threshold)
    pivot_doc_id = postings_lists[pivot_idx].current_doc_id()
    if pivot_term is None:
      break
    if pivot_doc_id <= current_doc_id:
      random_postings_list = random.choice(postings_lists[:pivot_idx])
      random_postings_list.next(current_doc_id + 1)
      continue
    else:
      if postings_list[0].current_doc_id() == pivot_doc_id:
        current_doc_id = pivot_doc_id
        score = compute_score(Query, current_doc_id, document_collection)
        if len(top_k) < k:
          heapq.heappush(top_k, (score, current_doc_id))
        elif score > top_k[0][0]:
          heapq.heappushpop(top_k, (score, current_doc_id))
          threshold = top_k[0][0]
      else:
        random_postings_list = random.choice(postings_lists[:pivot_idx])
        random_postings_list.next(pivot_doc_id)

下面我们再用一个例子来详细说明WAND的过程

假设我们的Query是”猫 狗 老鼠”，求解Top2，

在最初的情况下，因为堆为空，所以我们的阈值为0。

假定

猫在整个文档集合中最大的得分为0.1

狗在整个文档集合中最大的得分为0.4

老鼠在整个文档集合中最大的得分为0.9。

初始状态如下图所示

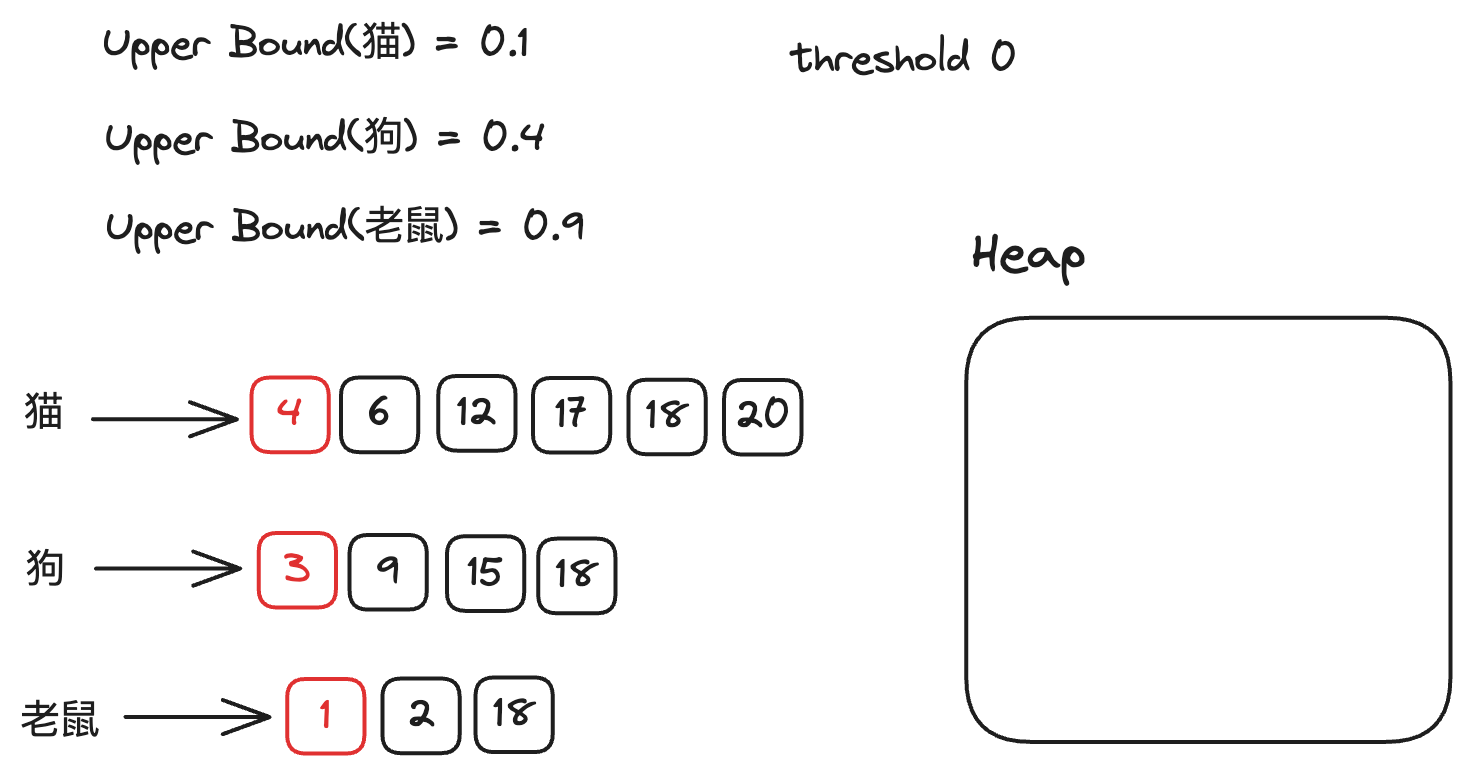
下面我们开始检索，对倒排链表按照Doc ID进行排序。从第一条倒排链开始，我们把对应term的upperbound 加到当前的得分上，得分为0.9。因为0.9 大于阈值0， 所以我们计算这个Doc真正的得分(0.6)，将其放入堆中。并将对应的倒排链移动到下一个文档。

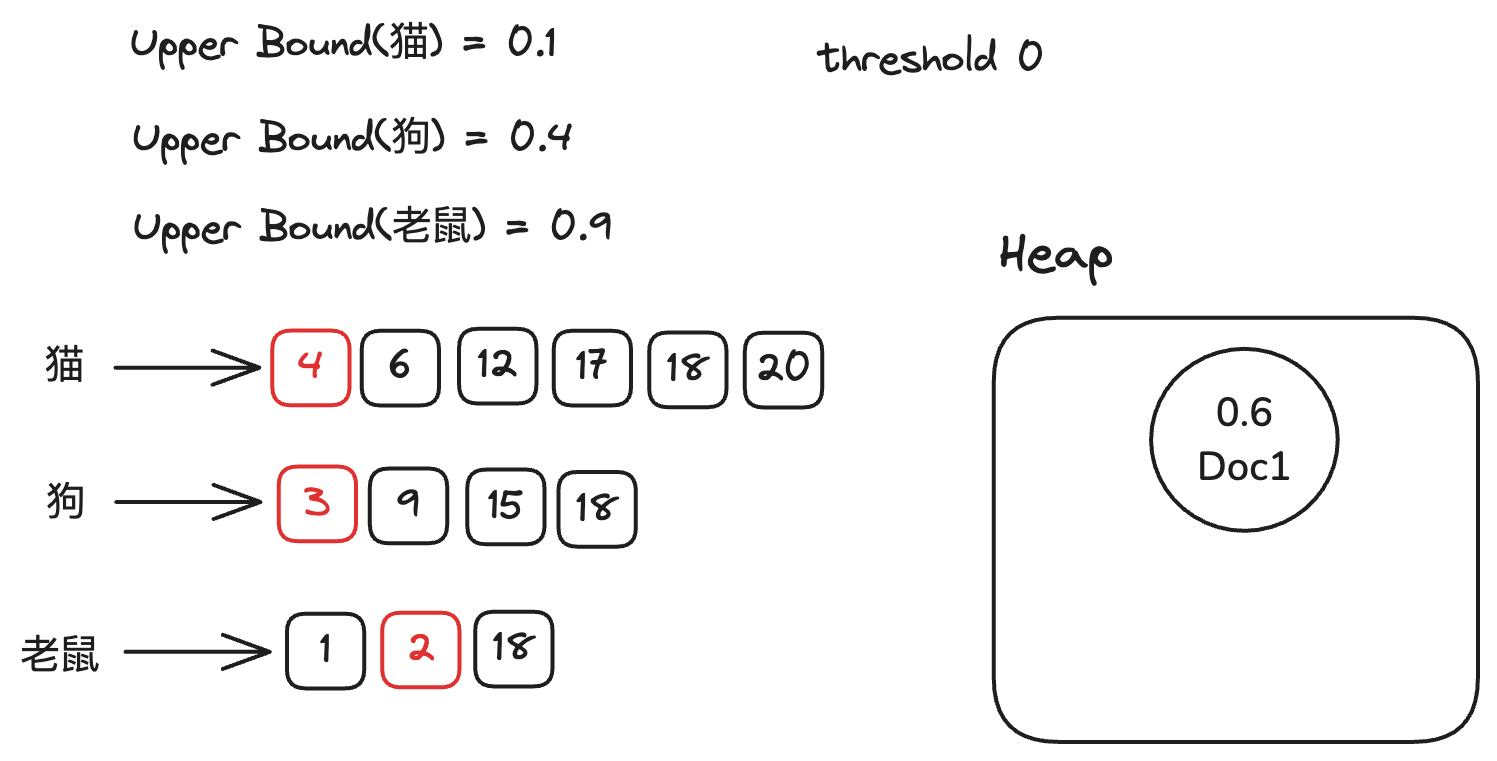
然后我们继续对倒排链表进行排序，继续从第一条倒排链开始。我们把老鼠的upperbound 加到当前的得分上，得分为0.9。因为0.9 大于阈值0， 所以我们计算这个Doc真正的得分(0.7)，将其放入堆中。 并将对应的倒排链移动到下一个文档。

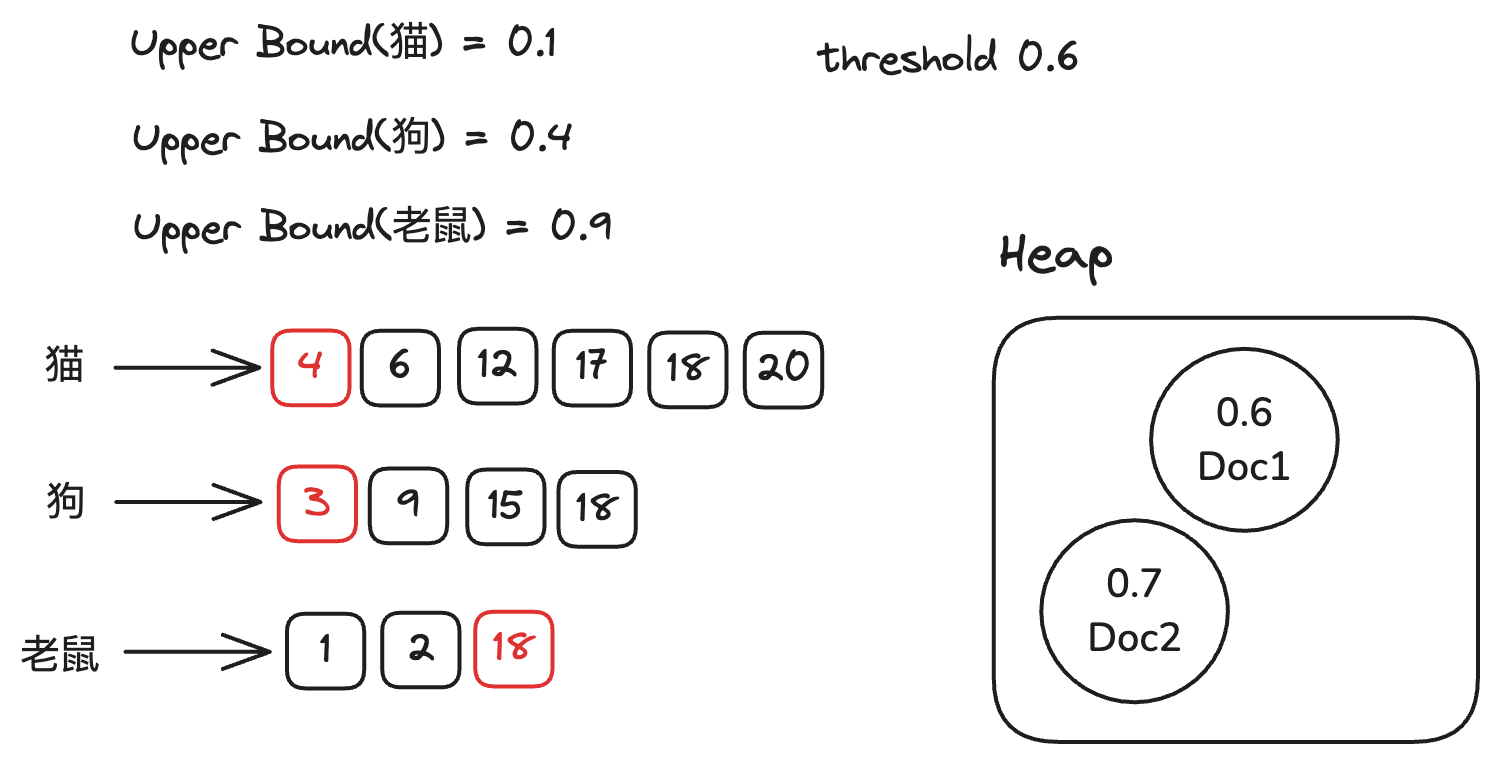
我们仍然对倒排链表进行排序, 然后从第一条倒排链开始，此时因为我们堆中已经有两个文档，所以我们的阈值为0.6。我们 从猫的倒排链开始，把猫的upperbound 加到当前的得分上，因为0.1 小于阈值0.6，所以我们需要继续累加狗的upperbound(0.4)。 直到当我们累加老鼠的upperbound时，我们的得分超过阈值。此时我们需要对比当前倒排链的Doc ID与第一条倒排链(猫)的Doc ID，发现当前倒排链的Doc ID大于第一条倒排链的Doc ID， 因此我们可以将当前倒排链之前的所有倒排链的Doc ID都移动到大于等于当前倒排链的Doc ID。

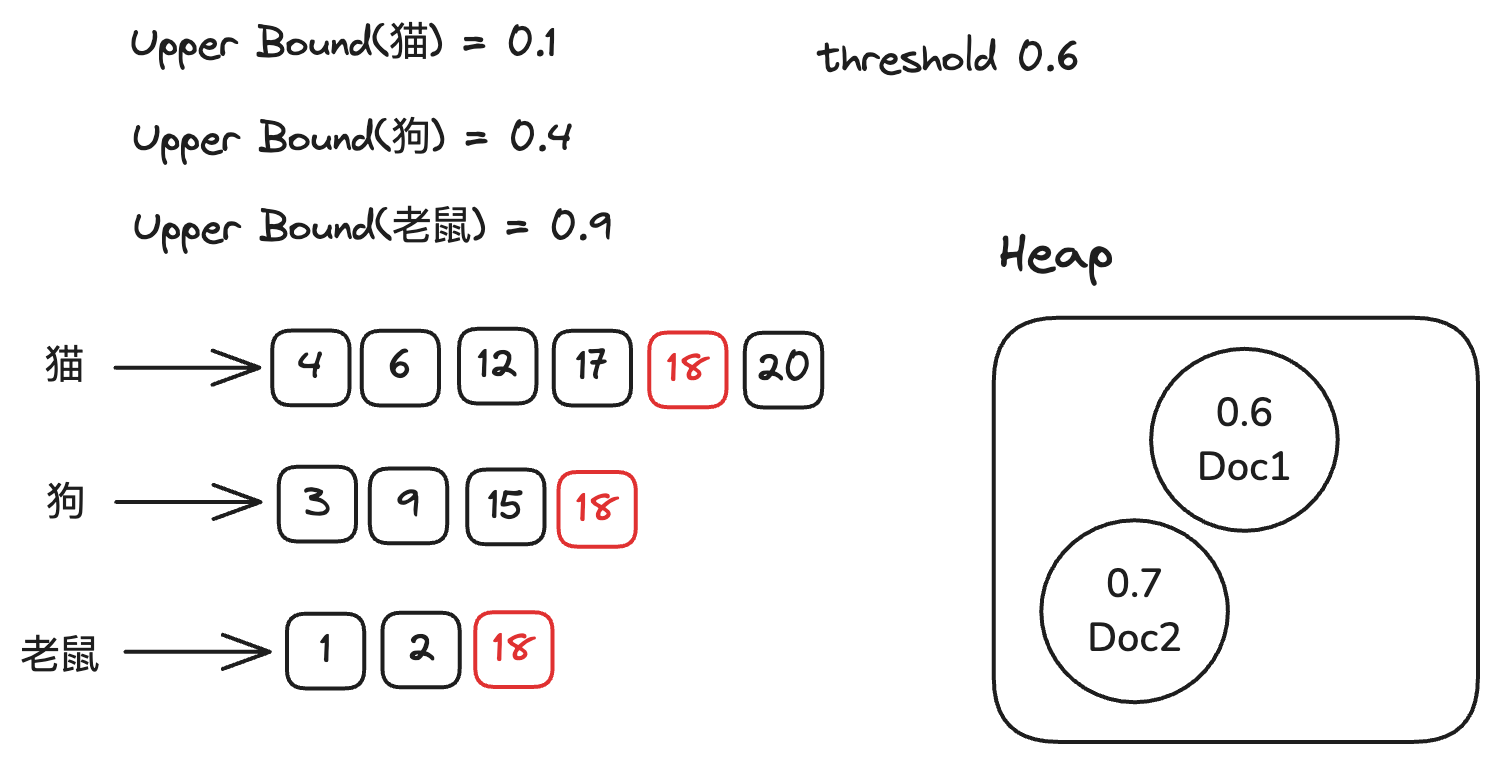
尽管WAND论文中提到的是在当前倒排链之前的所有倒排链中任选一个，将其Doc ID移动到大于等于当前倒排链的Doc ID， 这主要是出于担心所有倒排链一起移动会触发多次磁盘读取，但是实际上，我们可以将所有倒排链一起移动，这并不会影响正确性。

我们继续重复之前的步骤，这一次我们会发现当前倒排链的Doc ID与第一条倒排链(猫)的Doc ID相等，此时我们就找到了一个文档，我们计算它的得分(0.5)，然后与堆顶的文档进行比较，如果得分更高，那我们就将堆顶的文档替换为当前文档。 同时将对应的倒排链移动到下一个文档。下一轮我们会发现所有倒排链upperbound的和都小于阈值，因此我们可以结束检索，返回结果。

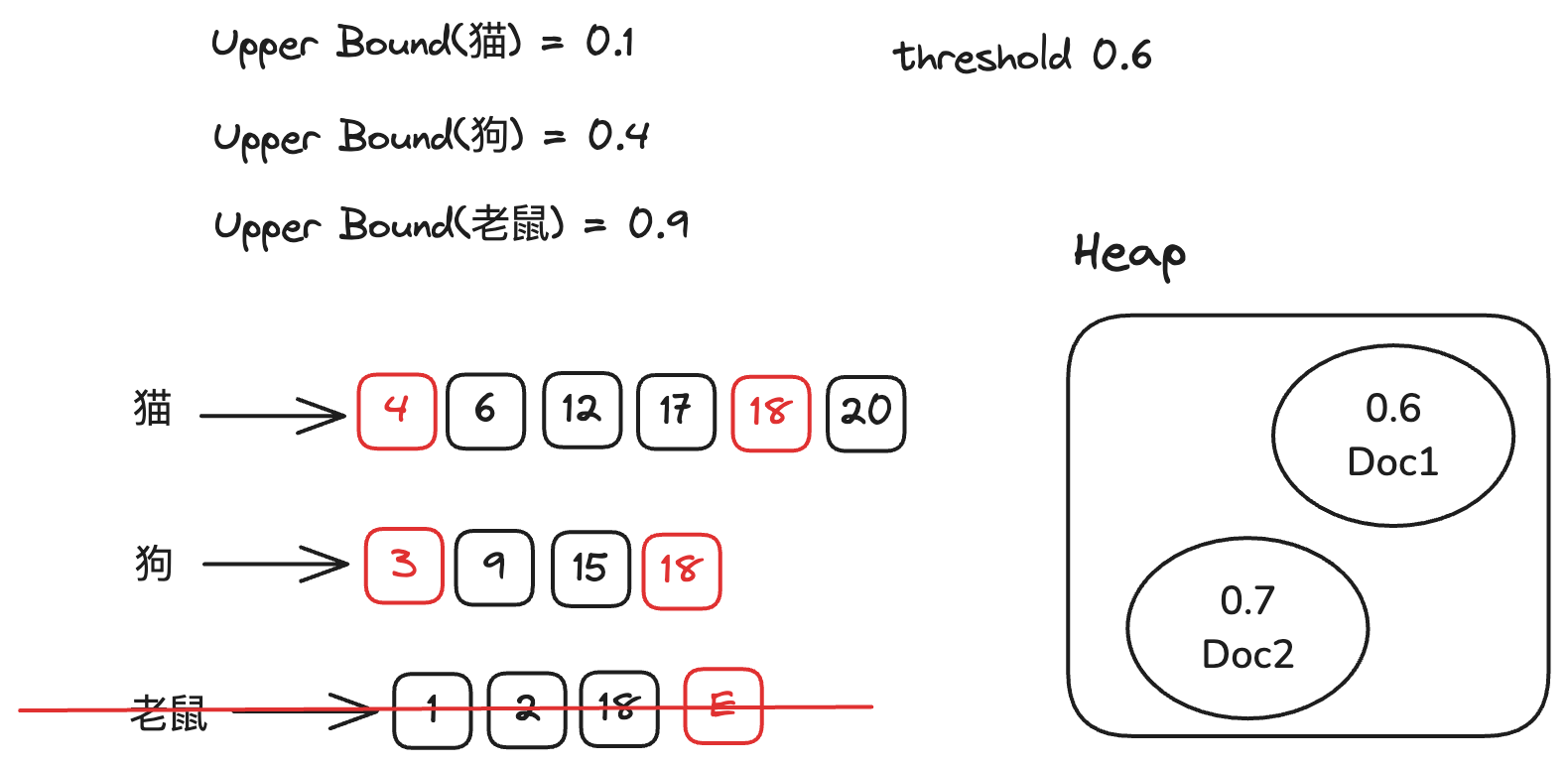
从这个例子中我们可以看到，WAND的优势在于，它可以在检索的过程中，根据当前的得分，动态的调整阈值，从而减少不必要的计算以及磁盘读取。(跳过了文档3，4，6，9，12，15，17)

MaxScore

MaxScore是一种基于DAAT的优化方法，它的特点是，我们会将倒排链分成两部分，一部分用来做OR检索，另一部分仅仅用来计算得分, 从而减少计算次数。它的具体步骤如下:

1. 对Query中的每一个term，我们检索出term对应的倒排链表
2. 我们将这些倒排链表按照upperbound倒序排序
3. 根据当前TopK的得分，我们将倒排链分成两部分：essential和non-essential
4. 对essential倒排链进行OR检索，得到一个文档ID, 再检查non-essential倒排链中是否包含这个文档ID，如果包含，将对应的term的得分加到当前文档的得分上
   1. 将文档的得分与堆顶的文档进行比较，如果得分更高，那我们将堆顶的文档替换为当前文档，并更新阈值，重复步骤3
   2. 如果得分没有超过阈值，重复步骤4

步骤3中的划分依据为，我们自下而上的累加upperbound，直到得分超过阈值。

假设此时的倒排链为i，那么我们将前i个倒排链作为essential倒排链，剩下的作为non-essential倒排链。 这样划分的好处是，一个Doc哪怕包含了non-essential倒排链中所有term，也不会成为TopK文档，因此我们只需考虑essential倒排链中的term。 从而减少计算次数。

伪代码如下

def split_postings_lists(postings_lists, threshold):
  """
  Split the postings lists into essential and non-essential parts.

  Args:
    postings_lists: A list of postings lists.
    threshold: The threshold score.

  Returns:
    A tuple (essential_postings_lists, non_essential_postings_lists) of the split postings lists.
  """
  essential_postings_lists = []
  non_essential_postings_lists = []
  score = 0
  # reverse for descending order
  i = len(postings_lists) - 1
  while i >= 0:
    score += postings_lists[i].upperbound
    if score > threshold:
      break
    non_essential_postings_lists.append(postings_lists[i])
  essential_postings_lists = postings_lists[:i] if i > 0 else []
  return essential_postings_lists, non_essential_postings_lists
def MaxScore(Query, document_collection):
  """
  Performs MaxScore retrieval.

  Args:
    Query: A list of Query terms (strings).
    document_collection: collection of documents to be searched.

  Returns:
    A list of (documentID, score) tuples, ranked in descending order of score.
  """

  inverted_index = document_collection.get_inverted_index()
  postings_lists = [inverted_index[term] for term in `Query`]
  top_k = []
  threshold = 0
  current_doc_id = None
  sort(postings_lists, key=lambda x: x.upperbound, reverse=True)
  while True:
    es_posting_list, unes_posting_list = split_postings_lists(postings_lists, threshold)
    doc_id = OR(essential_postings_lists)
    if doc_id in non_essential_postings_lists:
      score = compute_score(Query, doc_id, document_collection)
      if len(top_k) < k:
        heapq.heappush(top_k, (score, doc_id))
      elif score > top_k[0][0]:
        heapq.heappushpop(top_k, (score, doc_id))
        threshold = top_k[0][0]

下面我们再从一个例子来详细说明MaxScore的过程

假设我们的Query是”猫 狗 老鼠”，求解Top2， 假定

猫在整个文档集合中最大的得分为0.1

狗在整个文档集合中最大的得分为0.4

老鼠在整个文档集合中最大的得分为0.9。

下图为初始状态

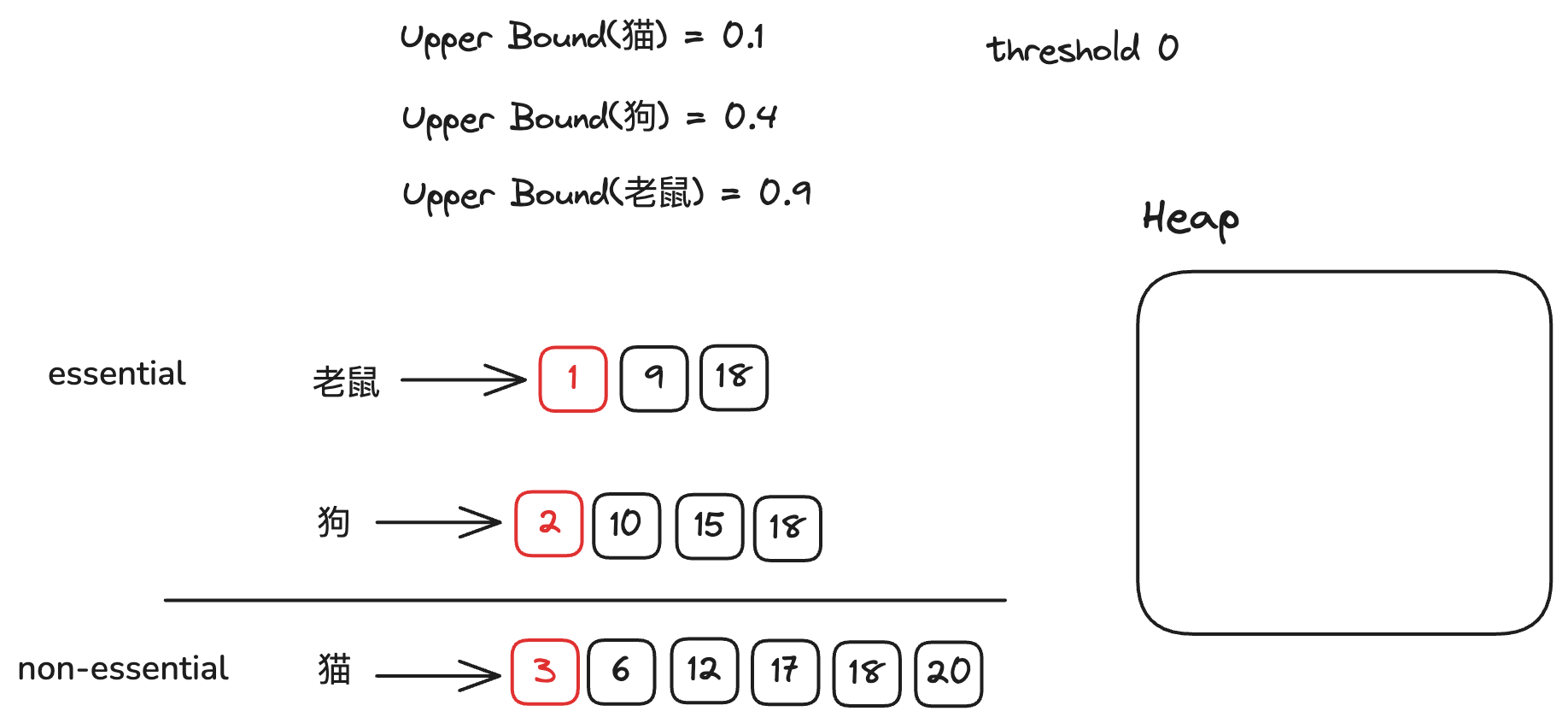
在最开始的情况下，我们的阈值为0，因此所有倒排链都是essential倒排链。 我们只需对Doc ID最小的文档进行算分，将其放入堆中。将对应的倒排链移动到下一个文档。

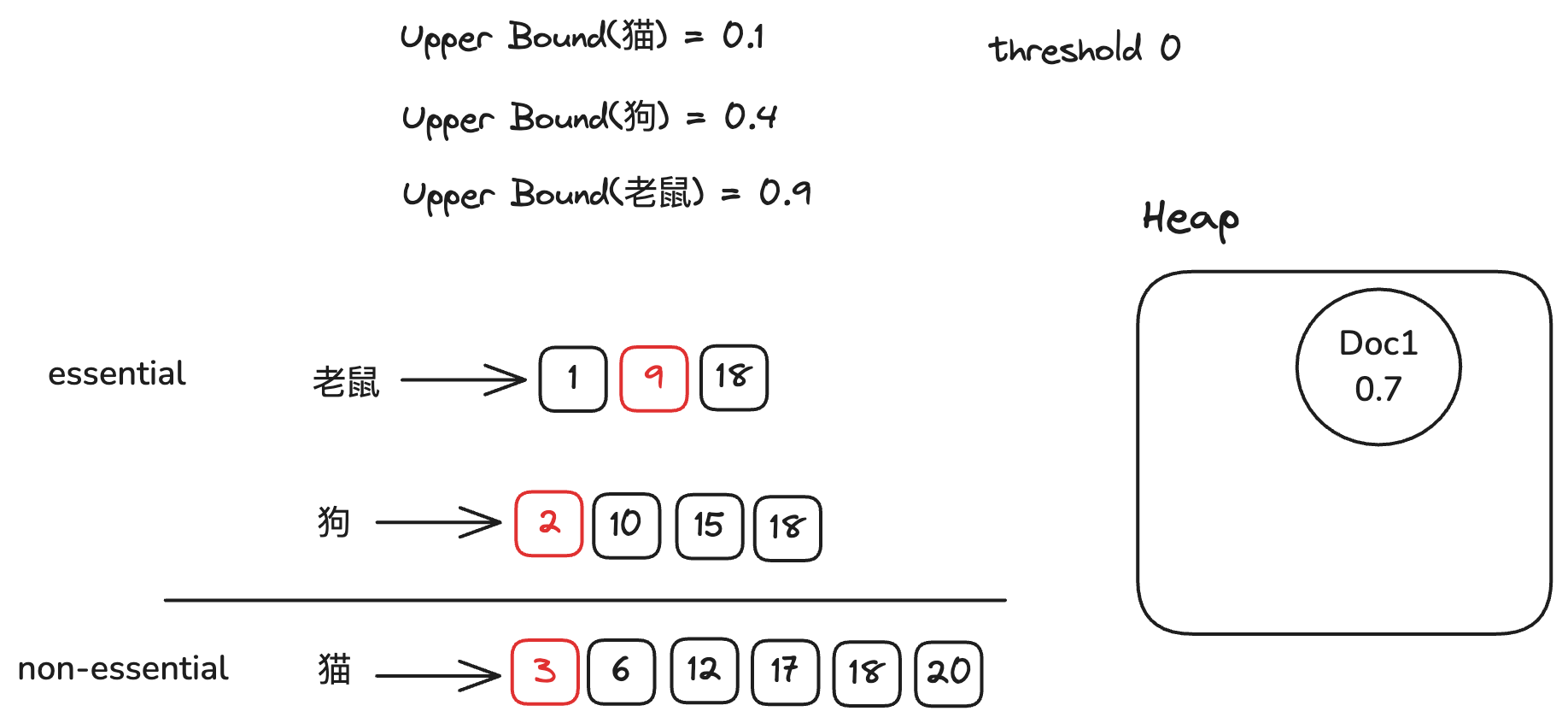
因为堆中的文档数小于2，我们的阈值依旧为0，因此我们继续对Doc ID最小的文档进行算分，将其放入堆中。然后我们将对应的倒排链移动到下一个文档。 此时堆的文档数等于2，我们更新阈值为0.3。

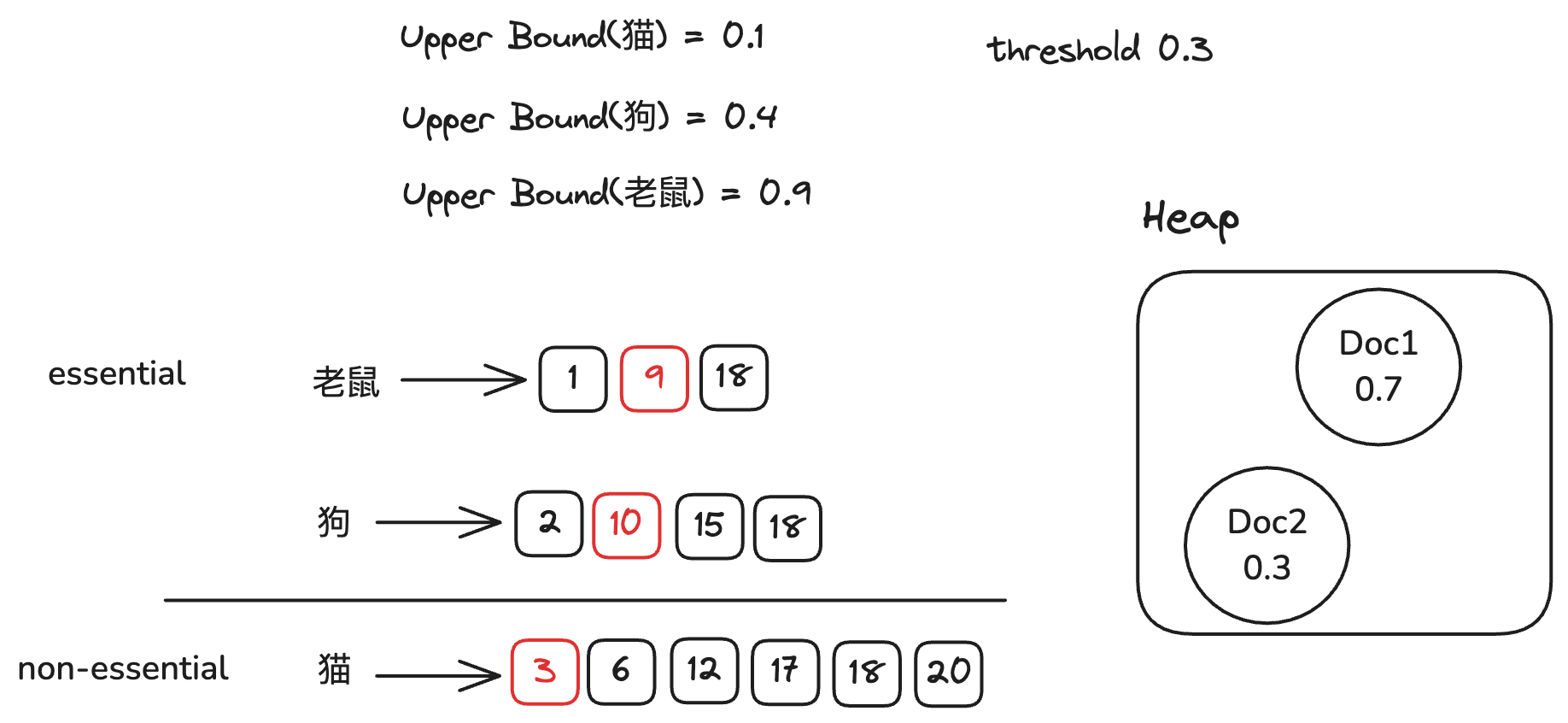
此时我们划分倒排链，我们发现猫的upperbound(0.1) + 狗的upperbound(0.4) = 0.5 > 0.3，因此我们将猫的倒排链划分为non-essential倒排链，狗和老鼠的倒排链作为essential倒排链。 我们对essential倒排链进行OR检索，得到文档9，因为non-essential倒排链中不包含文档9，因此我们计算文档9的得分(0.8), 更新TopK文档，更新阈值为0.7。

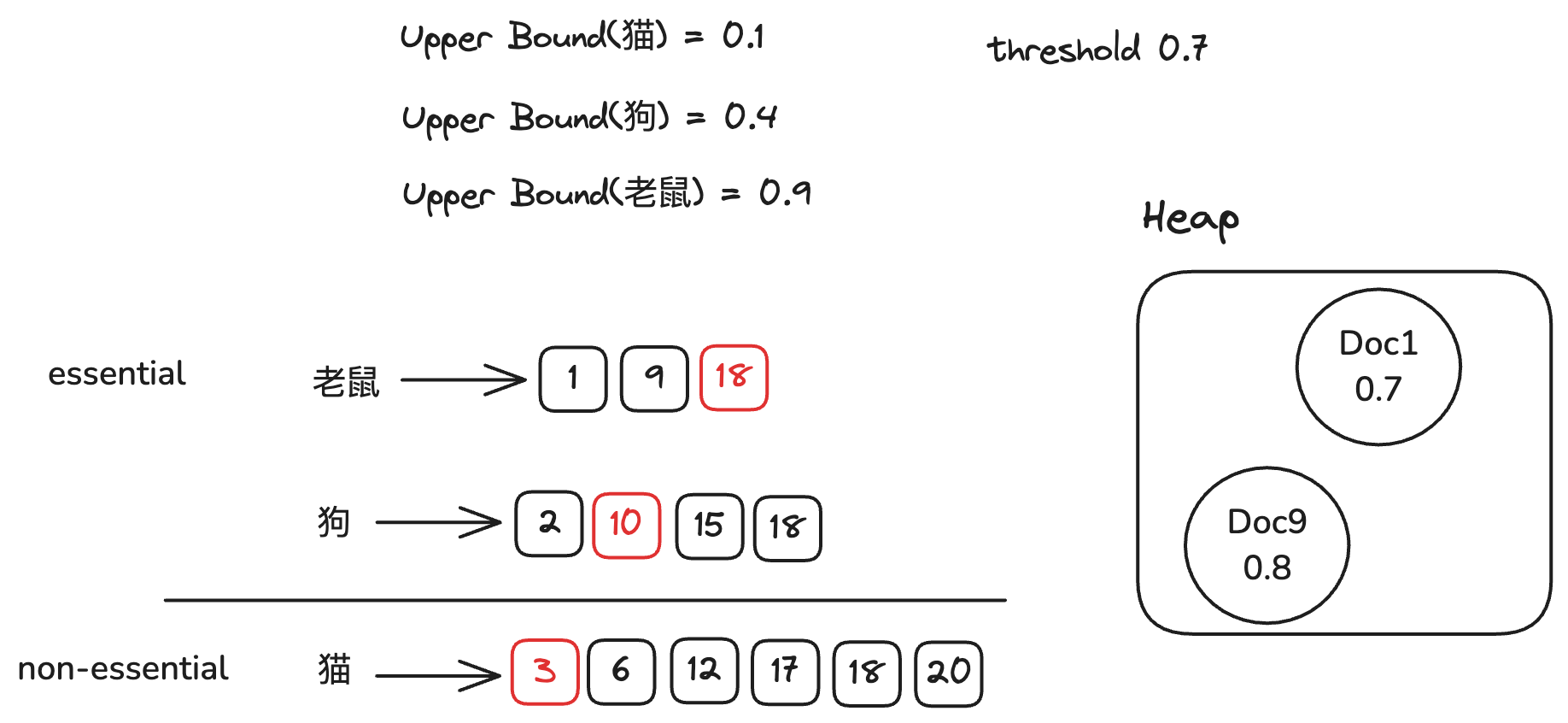
我们继续划分倒排链，此时需要将所有的倒排链全部加起来才能超过阈值，因此我们将猫和狗的倒排链划分为non-essential倒排链。 老鼠的倒排链作为essential倒排链。因为essential倒排链只有一条，我们直接遍历这条倒排链，得到文档18， 因为non-essential倒排链中包含文档18，计算文档18的得分(0.4), 无需更新TopK文档。

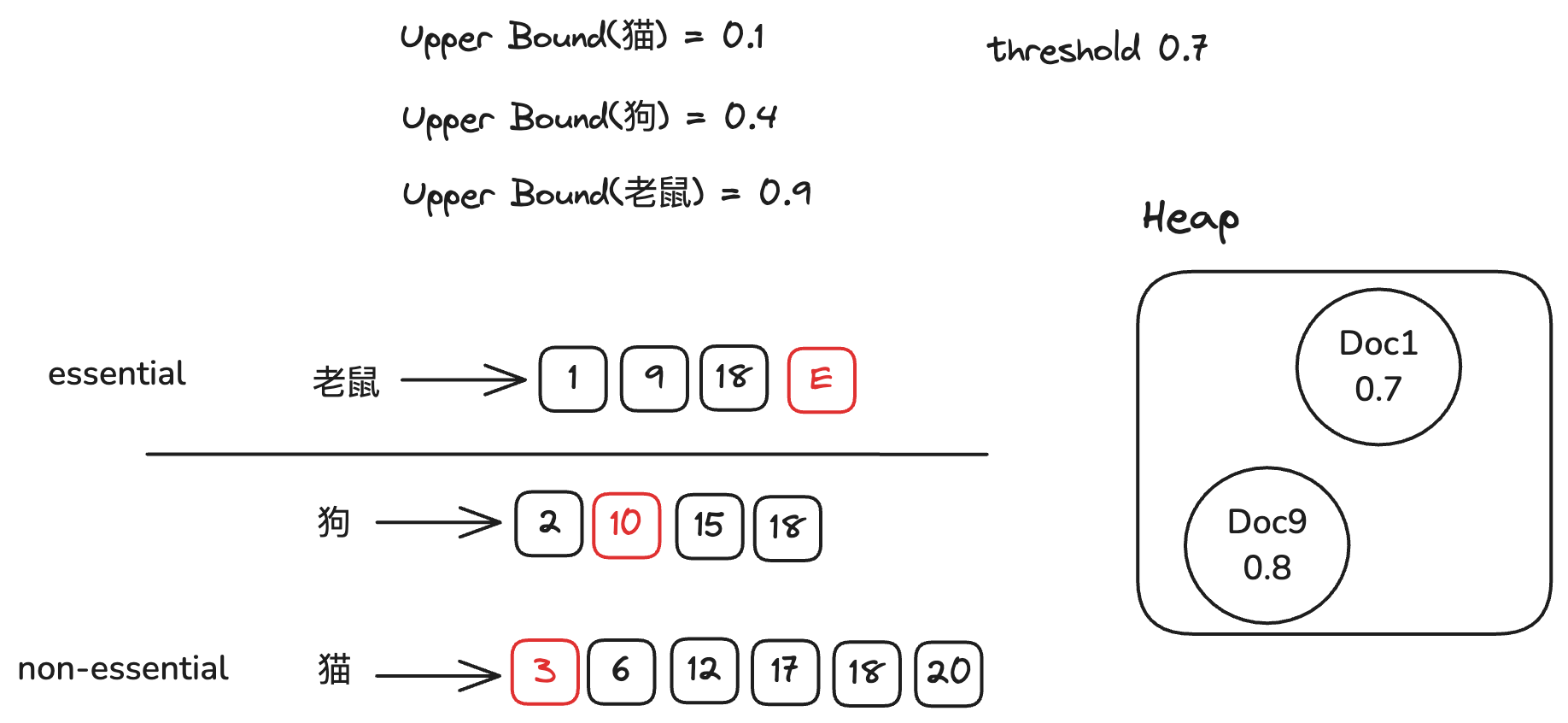
因为essential倒排链全部计算完毕，所以我们结束检索，返回结果。

Compare WAND and MaxScore

WAND和MaxScore都是基于DAAT的优化方法，它们的优势在于，可以根据当前的得分，动态的调整阈值，从而减少不必要的计算以及磁盘读取。 他们之间的优劣难以比较，在实际应用中，也无法说某一个方法一定比另一个方法好。 WAND相较于MaxScore的优势在于，它可以更激进的剪枝，从而减少计算次数。而它的劣势在于每一次检索时，都需要对倒排链进行排序 在Query较长时，排序的开销会变得很大。因此在Query较长时，MaxScore往往会比WAND更快。而在文档数量较大时，WAND往往会比MaxScore更快。

What’s Next

我们在这里仅仅简单介绍了检索中算分的一些简单方法，而更加进阶的BlockMaxScore，BlockMaxWAND等方法，留待以后的文章中介绍。