倒排索引是搜索引擎中最核心的数据结构之一，正因为有了倒排索引，搜索引擎才能高效地处理海量文本数据。目前工程里常见的实现大致有三类：

• 基于哈希表的倒排索引
• 基于FST的倒排索引
• 基于跳表的倒排索引

本文将首先介绍倒排索引不同实现方式的优缺点，然后重点介绍基于 FST 的倒排索引的原理及实现方式。

倒排索引的对比

首先我们先明确一下本文所说的倒排索引，它存储的键值对是什么? 在教科书中，我们会将term作为键，将包含该term的文档ID列表(posting list)作为值。如下图所示

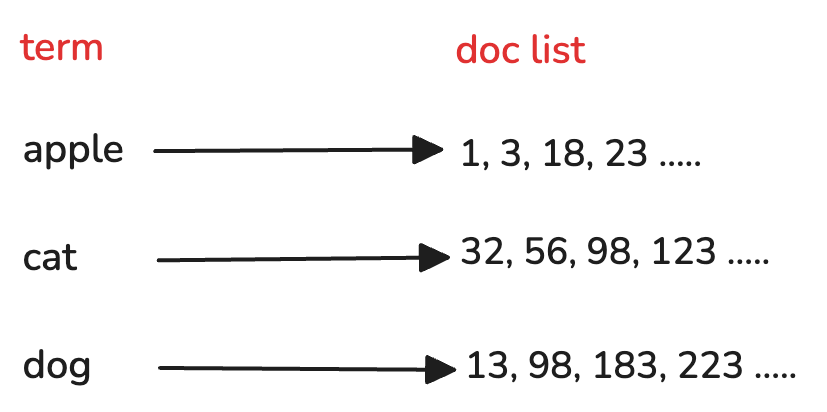
但是在具体实现中，我们往往并不会将整个文档ID列表存储在倒排索引中，因为文档数量非常庞大，如果把整个文档ID列表作为值存储在倒排索引中， 会导致倒排索引所需要的存储空间过大，无法常驻内存中，从而影响检索效率。因此倒排索引通常设计为两层结构。

• 第一层: 倒排索引, 存储term以及对应的文档ID列表在磁盘上的偏移位置(offset)
• 第二层: 磁盘上的文档ID列表, 存储实际的文档ID列表, 可以由倒排索引中的offset定位

大概的结构如下图所示

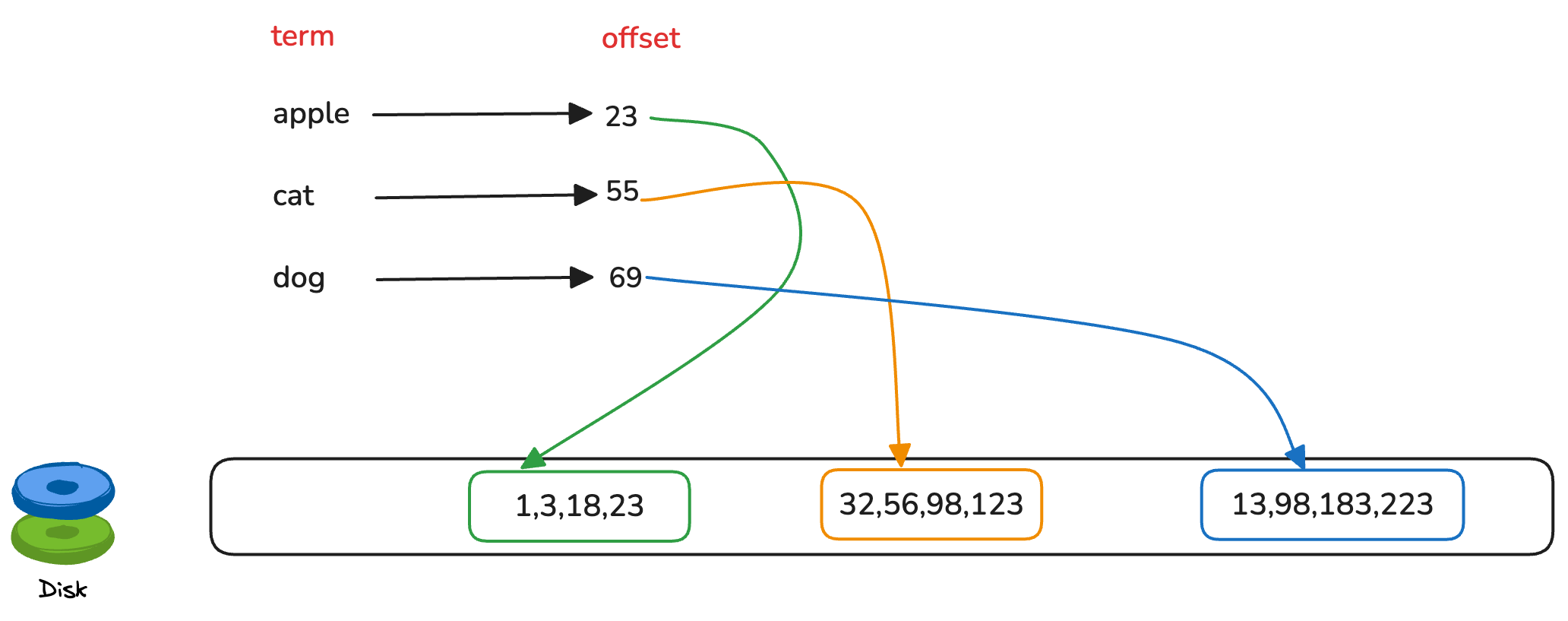
因此本文所说的倒排索引，实际上是指倒排索引的第一层结构。它的键值对为term以及对应的文档ID列表在磁盘上的偏移位置(offset)。 为了方便理解，我们假设倒排索引的数据结构，即为存储<string, int>的键值对.

在明确了这一点后，我们来对比一下不同实现方式的优缺点。

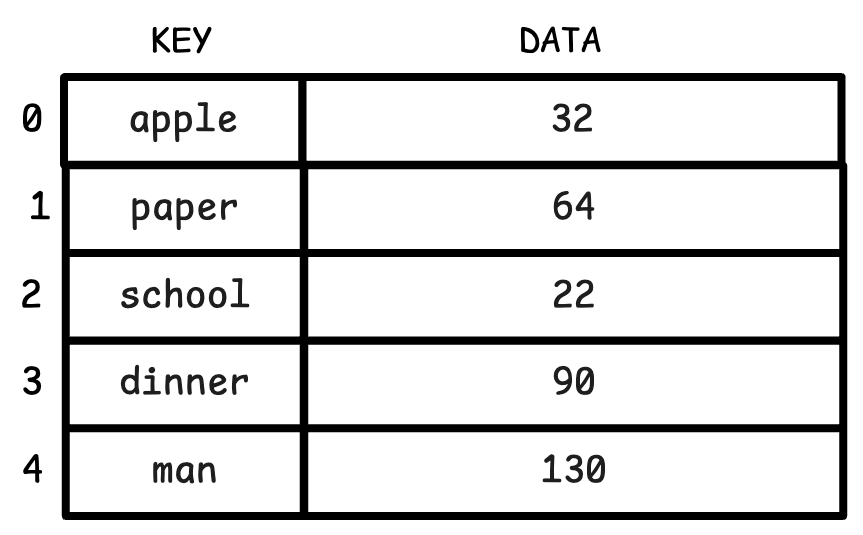
基于哈希表的倒排索引

使用哈希表实现倒排索引几乎是每个人的第一反应，因为这个使用场景完美契合哈希表的特点。 实际上，很多搜索引擎也的确是使用哈希表来实现倒排索引的。 但这种方式有一个天然短板，那就是哈希表无法高效的进行前缀搜索。

在搜索的场景中，前缀搜索是一个非常常见的需求。 例如，当用户在搜索框中输入”app”时，我们希望不仅能够匹配到”app”, 还希望搜索框中可以联想出”apple”, “application”等单词, 这样可以提升用户的搜索体验。可是由于哈希表并不是有序的，我们没有好的办法来进行前缀搜索。

不过哈希表的优势也明显：查找和构建都很快。

基于跳表的倒排索引

跳表有序，天然支持前缀/范围查询，因此，如果我们需要一个支持增删改的倒排索引，那么跳表是一个不错的选择。很多搜索引擎都会用跳表作为增量数据的倒排索引。 但是跳表相较于哈希表，查找速度会慢一些。

基于FST的倒排索引

FST 是Lucene中使用的倒排索引实现，但国内许多大厂自研的搜索引擎往往不使用 FST 作为倒排索引的实现方式，主要原因有以下几点:

• 认为FST速度不够快, 不符合高性能搜索引擎的要求
• FST对插入的顺序有要求，不支持实时的修改 (后面会详细说明)

但 FST 的优势也非常明显:

• 占用的内存非常小
• 支持高效的前缀搜索
• 速度适中, 它的时间复杂度为 O(m), m为term的最大长度, 与term的数量无关.

因此 FST 非常适合作为全量数据的倒排索引实现方式，尤其是在内存资源有限的场景下。

FST的概述与实现

下面我们来详细介绍 FST 的原理及实现方式. FST 可以被认为是一个压缩的 Trie 树。区别在于Trie树是通过复用前缀来节省空间，而FST在Trie树的基础上，更进一步，通过复用后缀进一步节省空间。

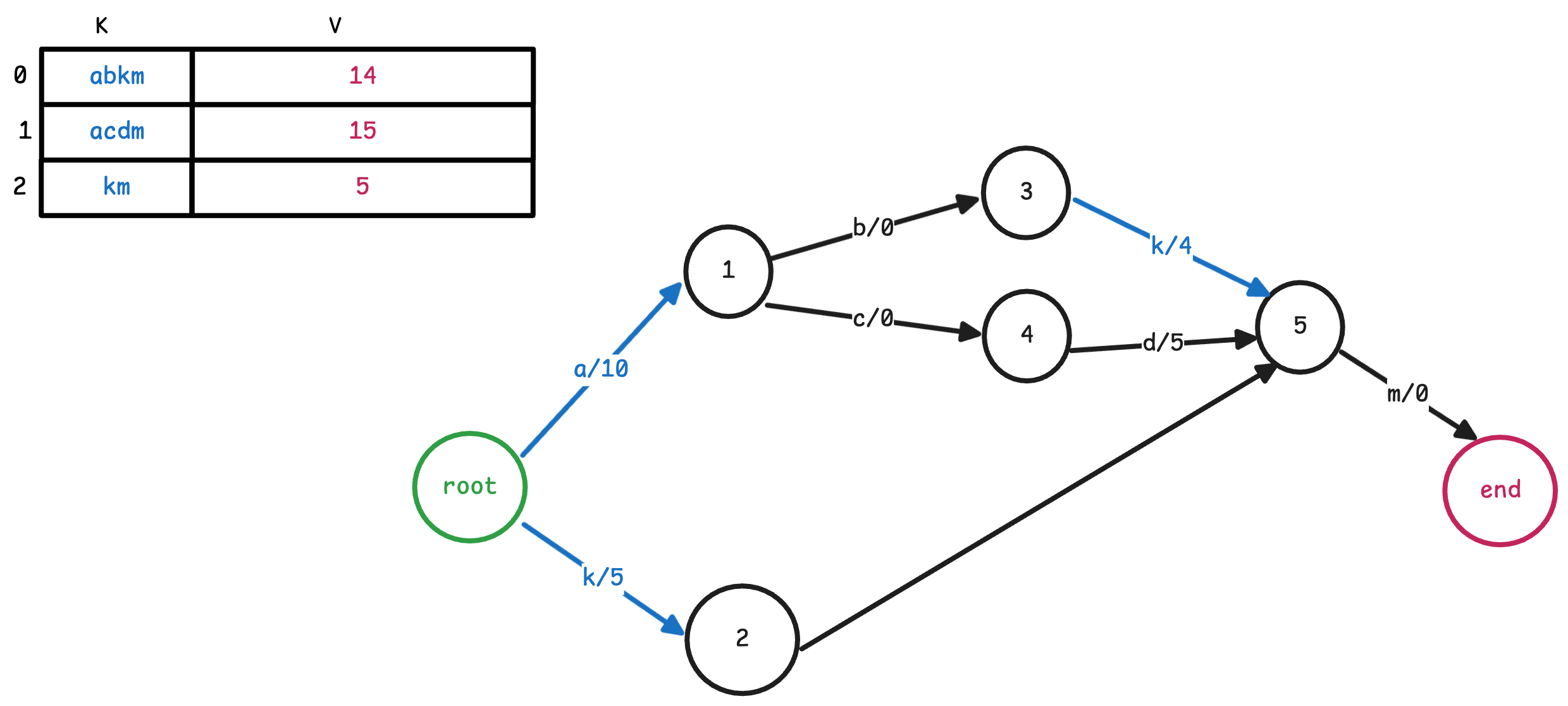
我们可以通过下面的图片来直观感受一下FST和Trie的区别.

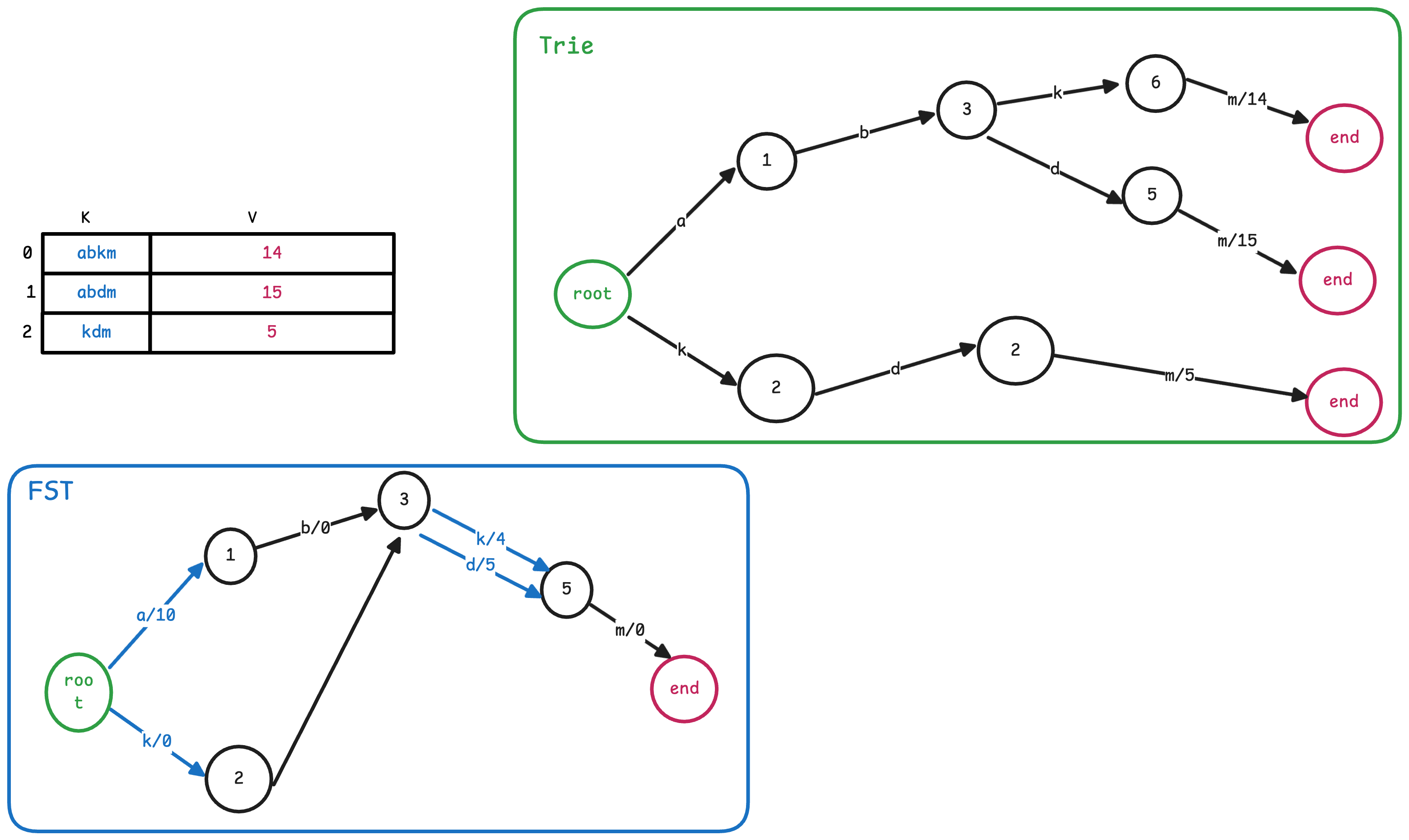
从图中我们可以看到，FST通过复用后缀，显著减少了节点的数量，从而节省了内存空间。但是从本质上来讲，FST和Trie是类似的，都是通过有向无环图(DAG)来存储字符串集合。 下面将分别从搜索和构建两个方面来介绍 FST 的原理。FST 的搜索显著简单于构建，因此我们先介绍搜索。

FST的搜索

在讲述FST的搜索之前，我们首先介绍一下组成FST的各个部分。

边

FST的边是有向的，从一个节点指向另一个节点。每条边都包含以下信息:

• label: 边的标签，表示这条边所代表的字符
• target: 这条边所指向的目标节点
• output: 这条边所携带的输出值(值 >= 0)

如果我们有一个 term cat，它对应的值为 5，那么它会变为三条边, 如下图所示

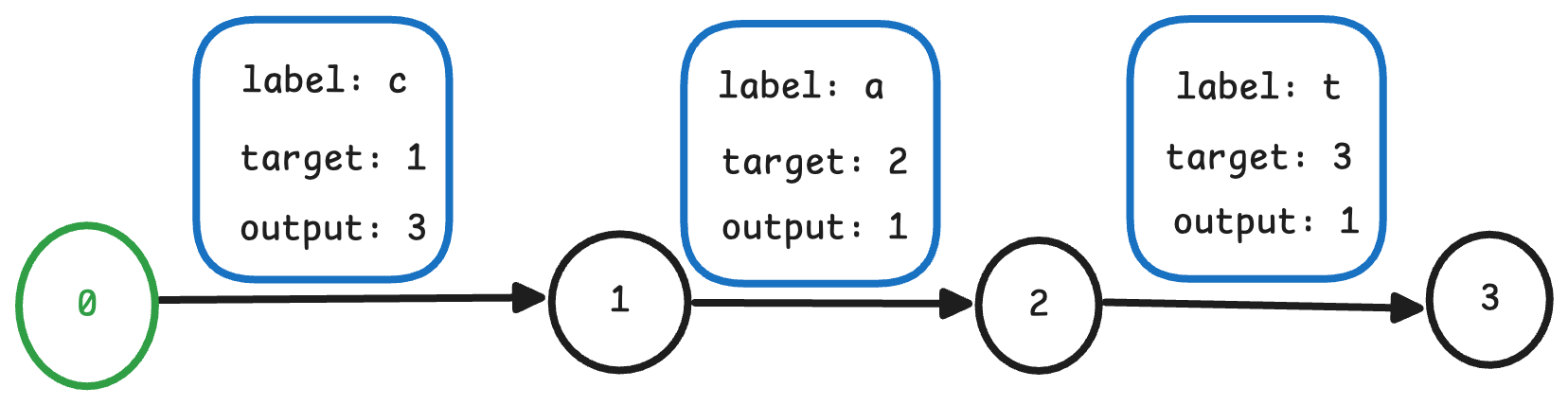
对于label 和 target, 这几个概念和Trie树是类似的，也比较直观。但 output 是 FST 所独有的，不同于Trie树将值存储在叶子节点上，FST将值分散的存储在各个边上。 需要将term对应的所有边的output进行累加，才能得到最终的值。

节点

FST的节点包含以下信息:

• arcs: 该节点的所有出边
• isFinal: 该节点是否为终止节点
• finalOutput: 如果该节点为终止节点，则在最终的输出中需要加上该值

对于arcs，它是一个边的有序列表，按照边的label 进行排序。 isFinal 则和Trie树的含义一样，表示该节点是否为一个完整的term的终止节点。可以用于判断一个term是否存在于FST中。

但 finalOutput 则看起来不直观，因为我们在前面介绍边的时候，已经说了FST会把term 对应的值分散存储在各个边上，那么为什么还需要在终止节点上存储一个 finalOutput 呢？

我们可以从下图的例子中看到我们为什么需要finalOutput。

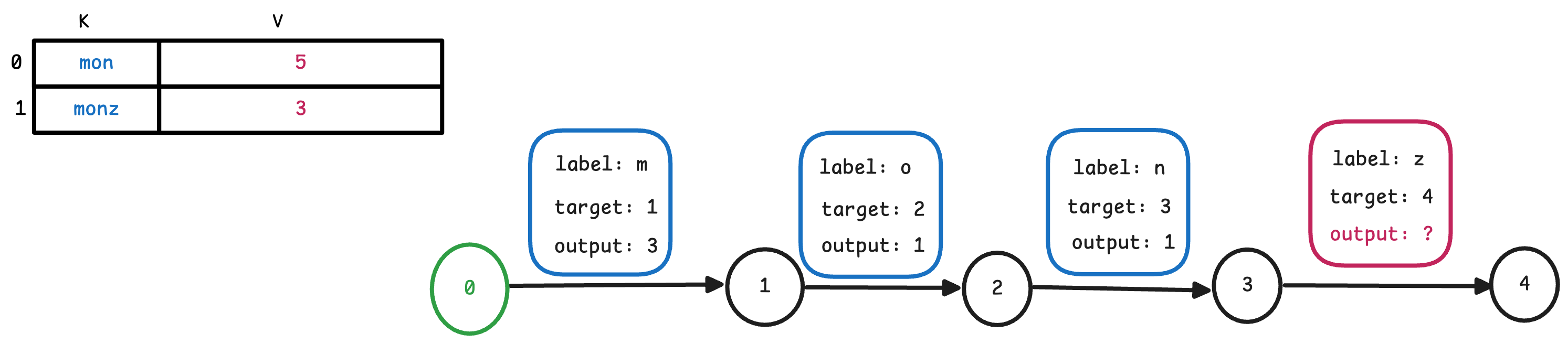
因为边的output 只能存储非负值，因此当我们遇到上述情况的时候发现，我们无法在满足 mon 的所有边上的 output 加起来等于 5， 同时又满足monz 的对应边上的output 加起来等于3。 因此我们需要在mon 终止节点上存储一个finalOutput，来解决这个问题。 如下图所示。

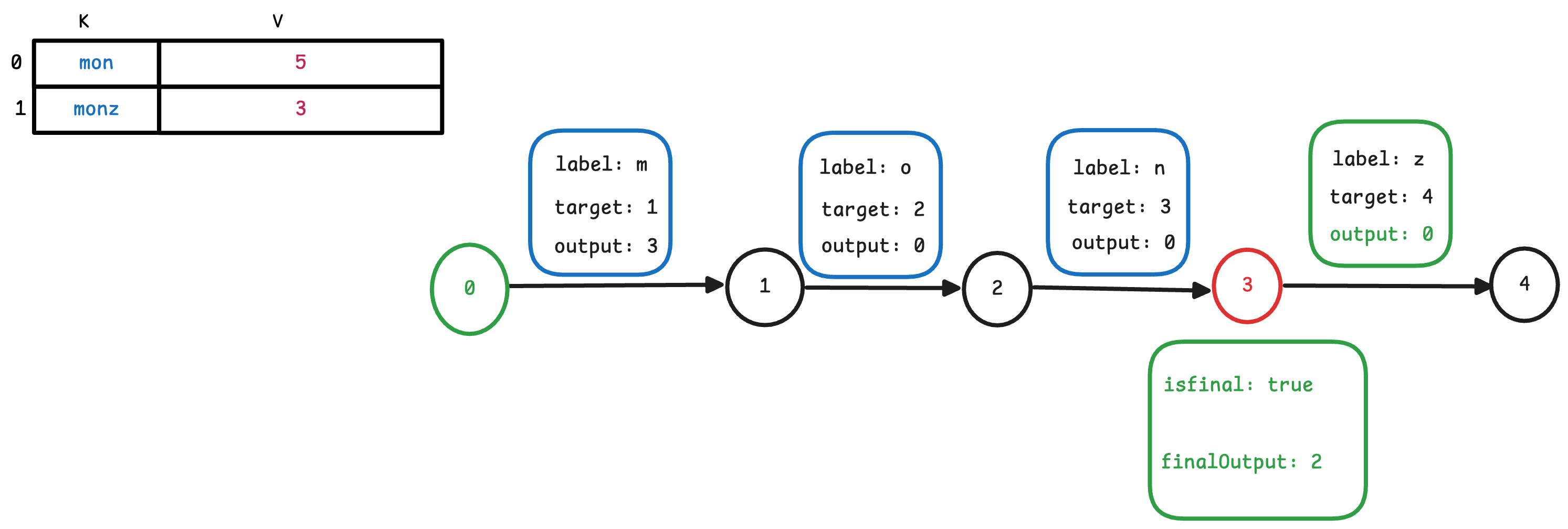
看到这里，大家可能会有疑惑，为什么output 不能是负数呢? 从实现上面来说，这完全是可以的。 在实现上，我们完全可以在边上存储一个负数。 这个非负数的限制，主要是为了减少存储空间。在实际的应用中，我们会将output 存储为变长整数(varint), 但变长整数对于负数的存储效率非常低， 因此选择将 output 限制为非负数，从而提升存储效率。

在介绍完FST的边和节点之后，其实搜索的算法过程也变得非常直观了。我们只需从根节点开始，依次查找每个字符对应的边，累加边上的output，直到遍历完整个term。如果最终停留的节点是一个终止节点，那么我们还需要加上该节点的finalOutput，最终得到的值即为该term对应的值。

整个搜索流程的伪代码/流程如下:

def search(fst, term):
    node = fst.root
    output = 0
    for char in term:
        arc = node.find_arc(char)
        if arc is None:
            return None
        output += arc.output
        node = arc.target
    if node.isFinal:
        output += node.finalOutput
        return output
    return None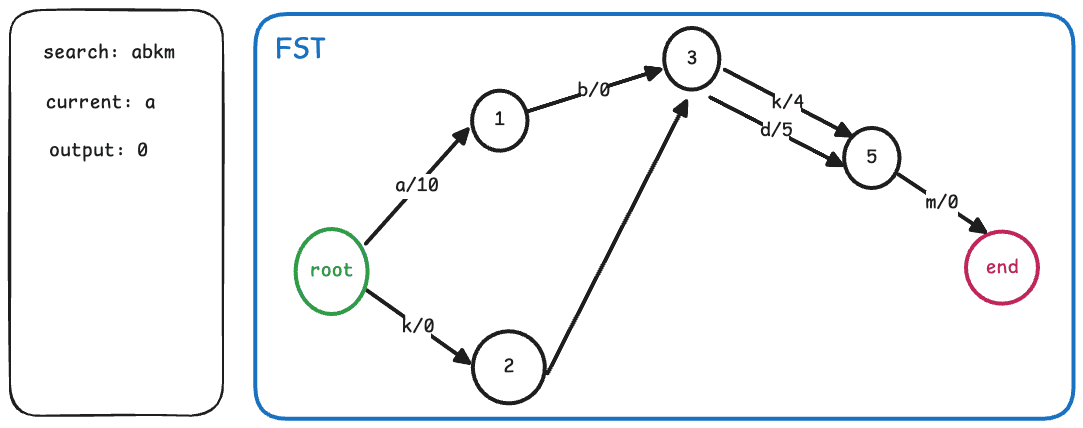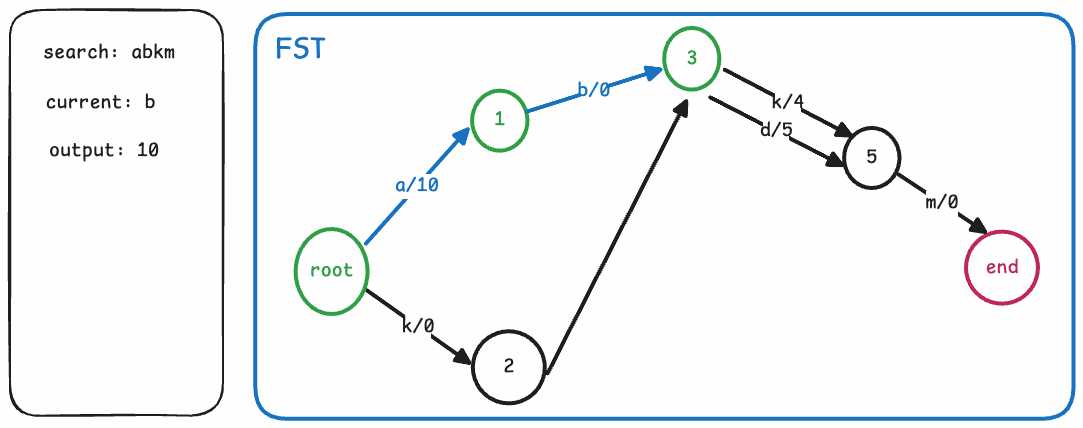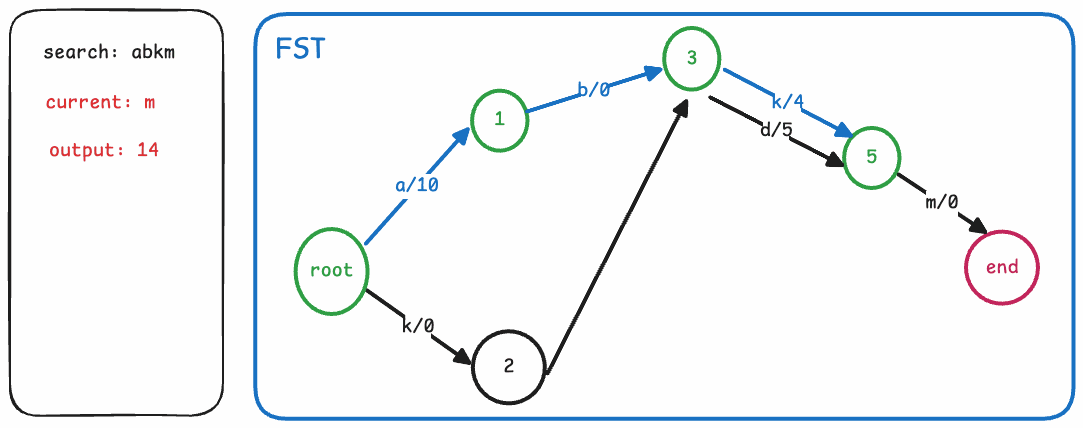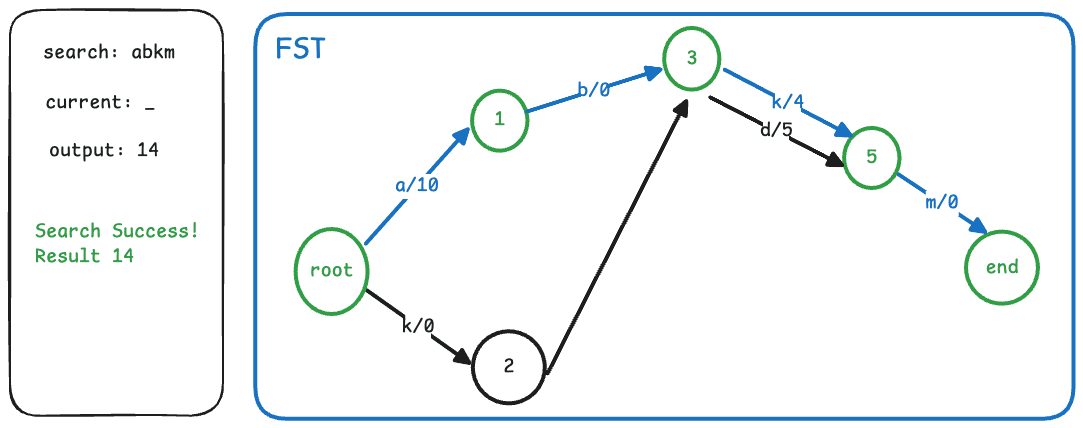

FST的构建

这一章节，我们讲述 FST 的构建过程。相较于搜索，构建复杂一些。本文不一上来给出完整算法，而是通过一个精心设计的小例子，逐步引入构建中涉及的关键概念，最后再回到整体流程。

假设我们有如下的 term 集合（已排序）及对应的值:

a     -> 5
ab    -> 2
cap   -> 1
tap   -> 1

为什么要求有序？ 有序能保证“上一个 term 的后缀部分不会再被修改”，因此可安全冻结（freeze）并参与后续复用。也正因为这一点，FST 不适合“实时逐条改写”，而适合批量构建。

我们从空的 FST 开始，依次插入每个 term。

1. 插入 a -> 5

第一条最简单，因为当前FST是空的，因此我们只需要创建一条边，连接根节点和一个终止节点即可，如下图所示:

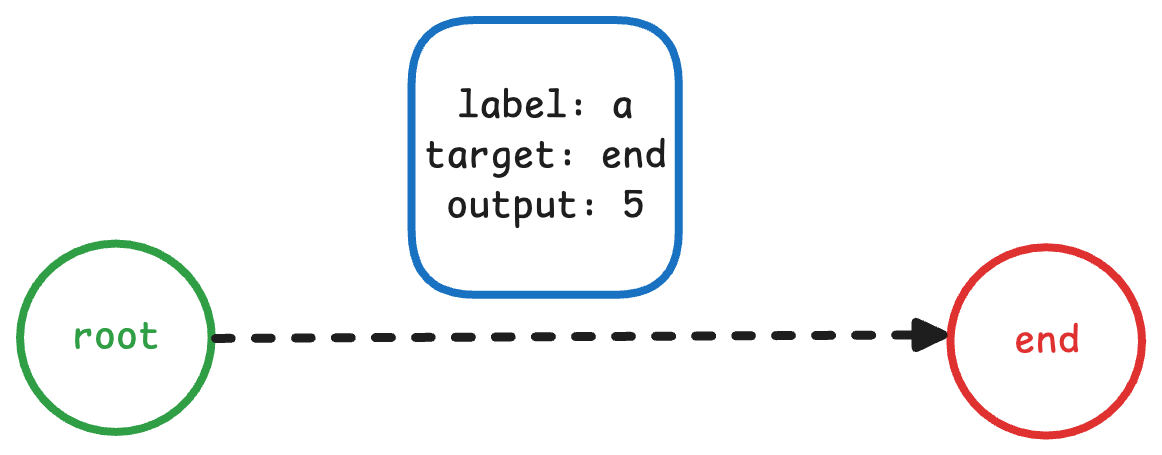
说明：虽然语义上只要“路径上弧输出相加 = term 值”即可，实现上会尽量把值放在开头的弧，实现更为简单。

2. 插入 ab -> 2

从这步开始进入完整流程。每次插入分为四步：

• 寻找前缀: 与上一条输入的最长公共前缀。
• 处理后缀: 把上一条在前缀之后的后缀冻结（以便复用）。
• 插入新的输入: 接下来，我们需要插入当前的输入。因为我们已经得到了前缀，所以我们只需要插入后缀部分即可。
• 调整输出: 对边的output进行调整，从而确保路径上的output 累加起来等于term对应的值。同时不会影响之前插入的term的值。

我们先看前三个步骤，然后再看最后一个步骤。

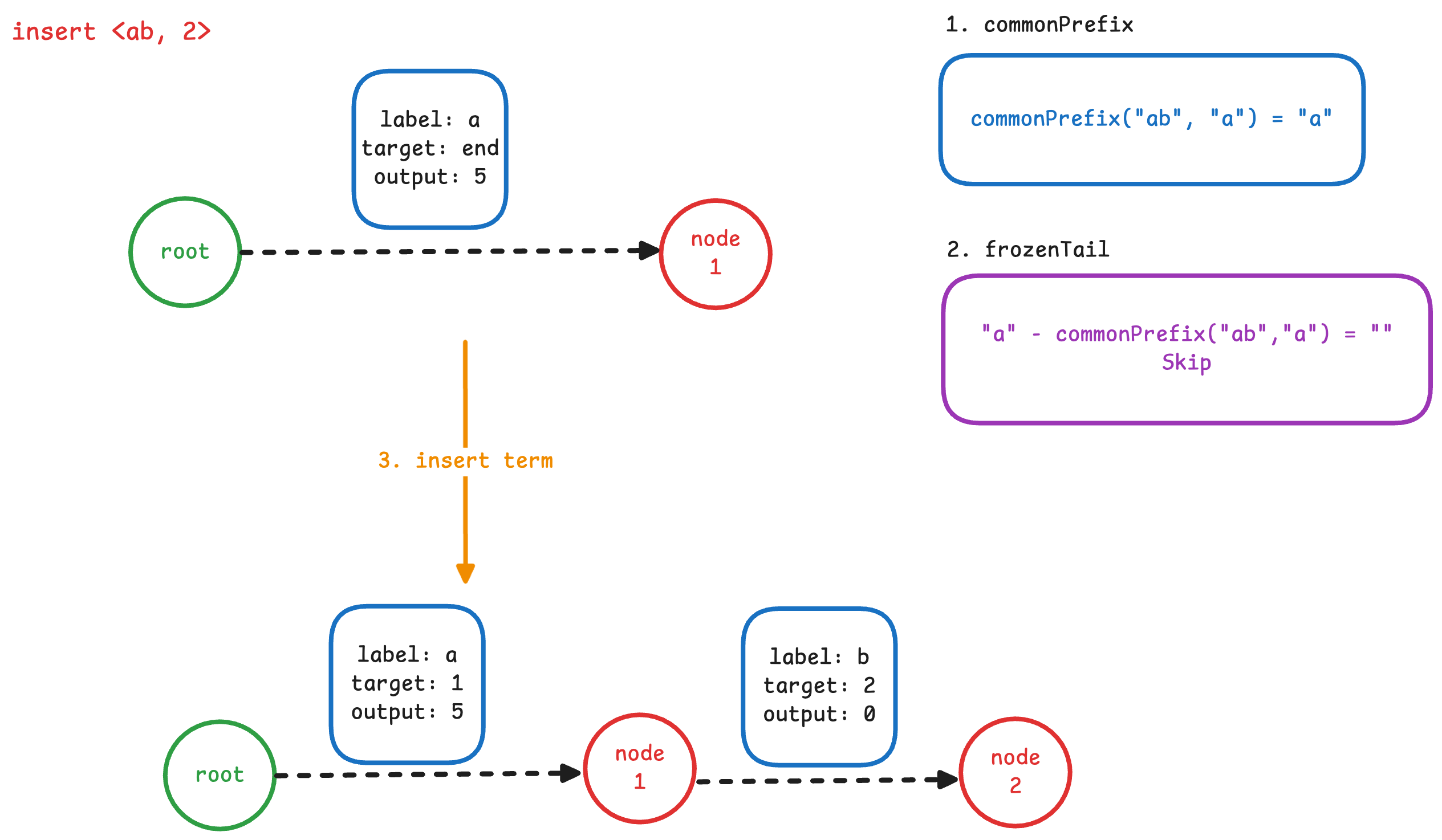
• 2.1 寻找前缀

在这个例子中，插入的 term 是 ab, 它与上一个插入的 term a 共有的前缀为 a。

• 2.2 处理后缀

因为找到的前缀 “a” 就是上一个插入的 term “a” 的全部内容，因此后缀为空，不需要进行冻结，可以直接跳过这一步。

• 2.3 插入新的输入

在前缀节点（图中 node 1）之后，插入后缀 b 与新的终止节点 node 2。新弧的 label为b、output为0。

• 2.4 调整输出

我们发现当把路径上边的 output 累加起来，对于”ab” 而言， 它的值并不等于2. 因此需要调整边的 output，使结果正确。

FST 的调整输出的算法直接描述比较复杂，这里提供一份伪代码，配合上面的例子，方便读者理解。

def prepend_output(child, prefix, outputs):
    """
    把 prefix加到 child 的所有弧上；
    若 child 在此为终止状态，还要再把 prefix 加到 child 的finalOutput上。
    - child.out_arc_outputs: 该子节点的所有出弧
    - child.is_final:        bool，child 是否为终止节点(final 为True)
    - child.final_output:    节点的finalOutput(前文已经介绍过这个概念)
    """
    for i in range(len(child.out_arc_outputs)):
        child.out_arc_outputs[i] = outputs.add(prefix, child.out_arc_outputs[i])
    if child.is_final:
        child.final_output = outputs.add(prefix, child.final_output)


def adjust_output_once(parent, child, residual):
    """
    在共享前缀的 parent child 节点之间调整输出
    - parent:     父节点
    - residual:   新插入的term剩余output
    - child:      子节点
    """
    # 1) 取父节点最后一条弧的 output 与 residual 的公共output， 对于整数而言，就是取最小值
    parent_last_arc_output = parent.arcs[-1].output
    common = outputs.common(residual, parent_last_arc_output)
    parent.arcs[-1].output = common

    # 2) 旧弧多出来的那部分下沉到 child（影响其所有弧与终止）
    word_suffix = outputs.subtract(parent_last_arc_output, common)
    if word_suffix != outputs.NO_OUTPUT:
        prepend_output(child, word_suffix, outputs)

    # 3) 新键自己的剩余输出也去掉公共部分，带去下一台阶
    new_residual = outputs.subtract(residual, common)

    return new_residual

def adjust_output(parent, child, residual, prefix):
    """
    递归地在共享前缀的 parent child 节点之间调整输出
    - parent:     父节点, 初次调用时为根节点
    - residual:   新插入的term剩余output
    - child:      子节点
    - prefix:     共享前缀
    """
    for i in range(len(prefix)):
        residual = adjust_output_once(parent, child, residual)
        if residual == outputs.NO_OUTPUT:
            break
        # 继续往下调整
        parent = child
        child = child.arcs[-1].target
    child.arcs[-1].output = residual

根据上面的伪代码，在这个例子中，我们先处理共享前缀的部分。

调整 node 0 和 node 1 之间边的 output。我们发现 node 0 的最后一条边的 output 为 5, 而需要插入的 term “ab” 的 output 为 2, 因此它们的公共部分 (min) 为 2， 因此我们将 node 0 和 node 1 之间边的 output 调整为 2。

然后将多出来的部分 3 下沉到 node 1 上，因为 node 1 是终止节点，因此需要将 3 加到 node 1 的 finalOutput 上。 同时 node 1 的所有出边的 output 也需要加上 3。 如下图所示:

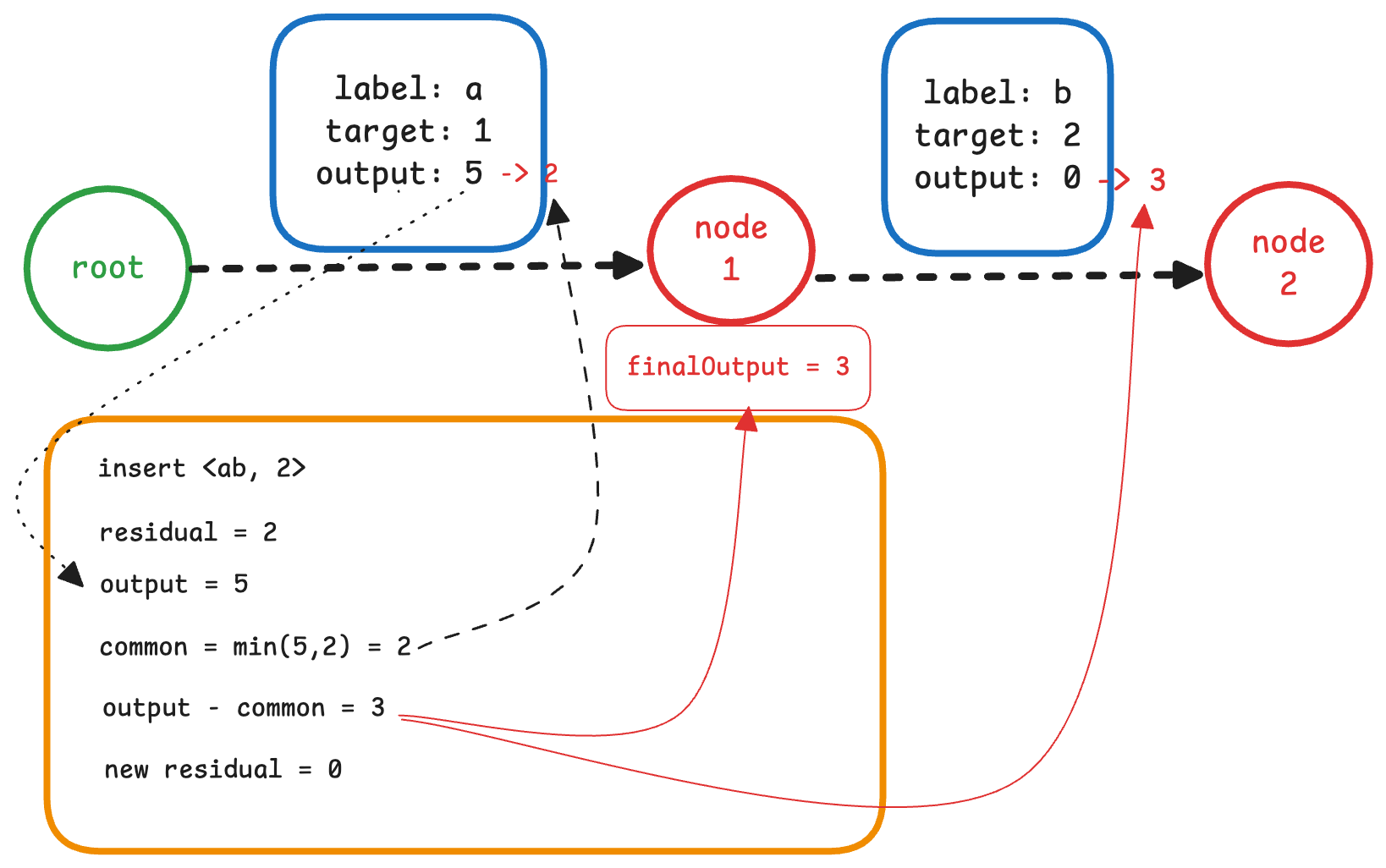
在处理完共享前缀的部分后，直接将分叉后最后一条边的 output 设置为新的 residual 即可。如下图所示:

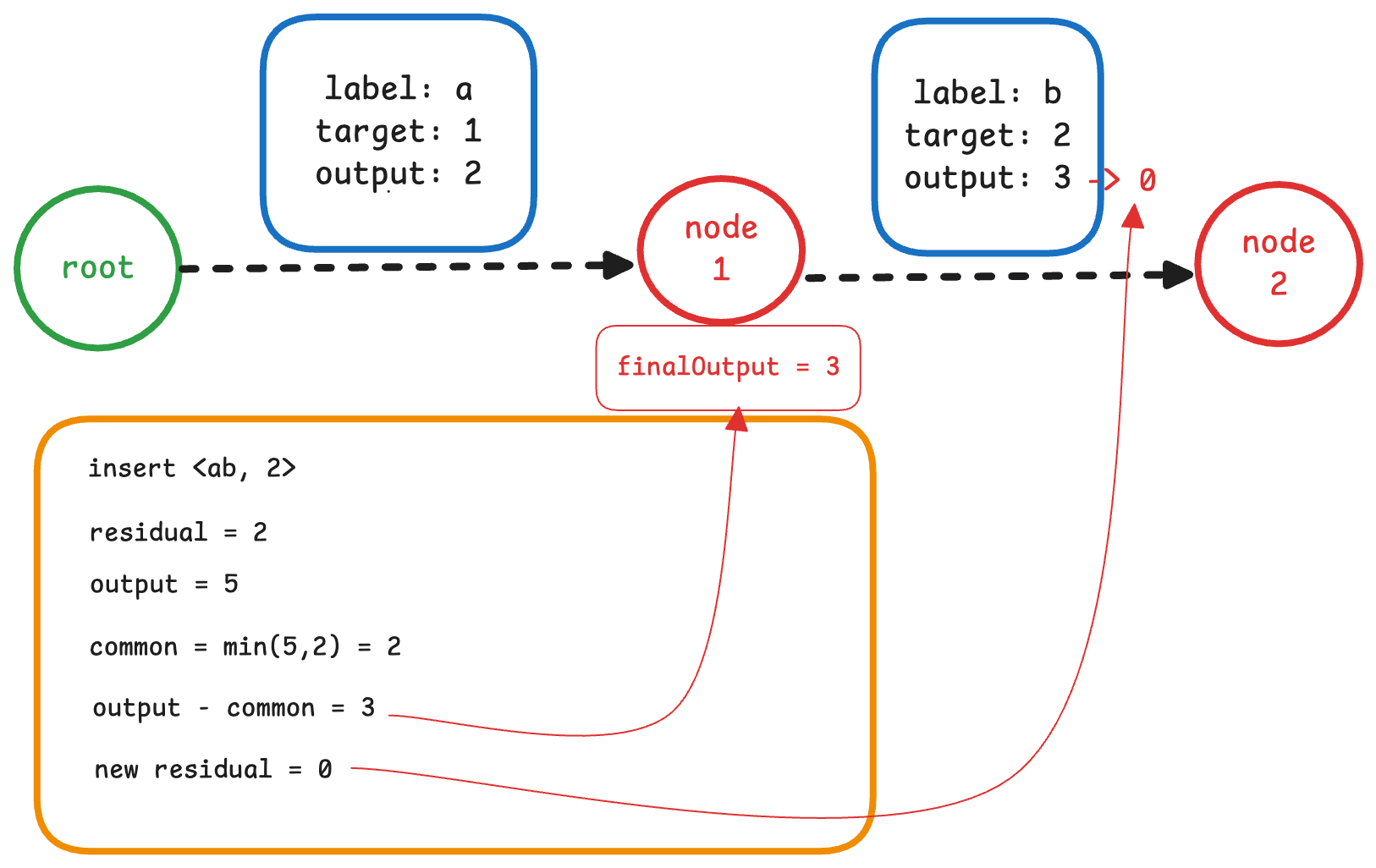
完成上述四个步骤后，我们成功地将 ab -> 2 插入到了 FST 中。

3. 插入 cap -> 1

• 3.1 寻找前缀

插入的 term 是 cap, 它与上一个插入的 term ab 共有的前缀为空。

• 3.2 处理后缀

因为找到的前缀为空，因此上一个term的后缀部分 “ab” 仍然存在，需要将其进行冻结 (freeze)。 冻结的过程为，将 需要冻结的节点所包含的信息进行哈希，然后检查是否已经存储了相同的节点，如果存在，就复用该节点，否则就将该节点存下来(称之为compiledNode)。

举一个例子，假设需要冻结的节点包含以下信息:

• arcs:
  • label: b, target: end, output: 0
• isFinal: True
• finalOutput: 0

这些信息哈希后, 得到一个 hash 值, hash1。 后续构建过程中，如果发现一个节点，它的 hash 值也是 hash1, 那么就可以复用之前存储的节点. 这样就实现了节点的复用，从而节省了内存空间。

• 3.3 插入新的输入

接下来，我们需要插入term 的后缀部分 “cap”。因为找不到任何前缀，因此需要从根节点开始，依次插入三条边以及一个终止节点。 如下图所示:

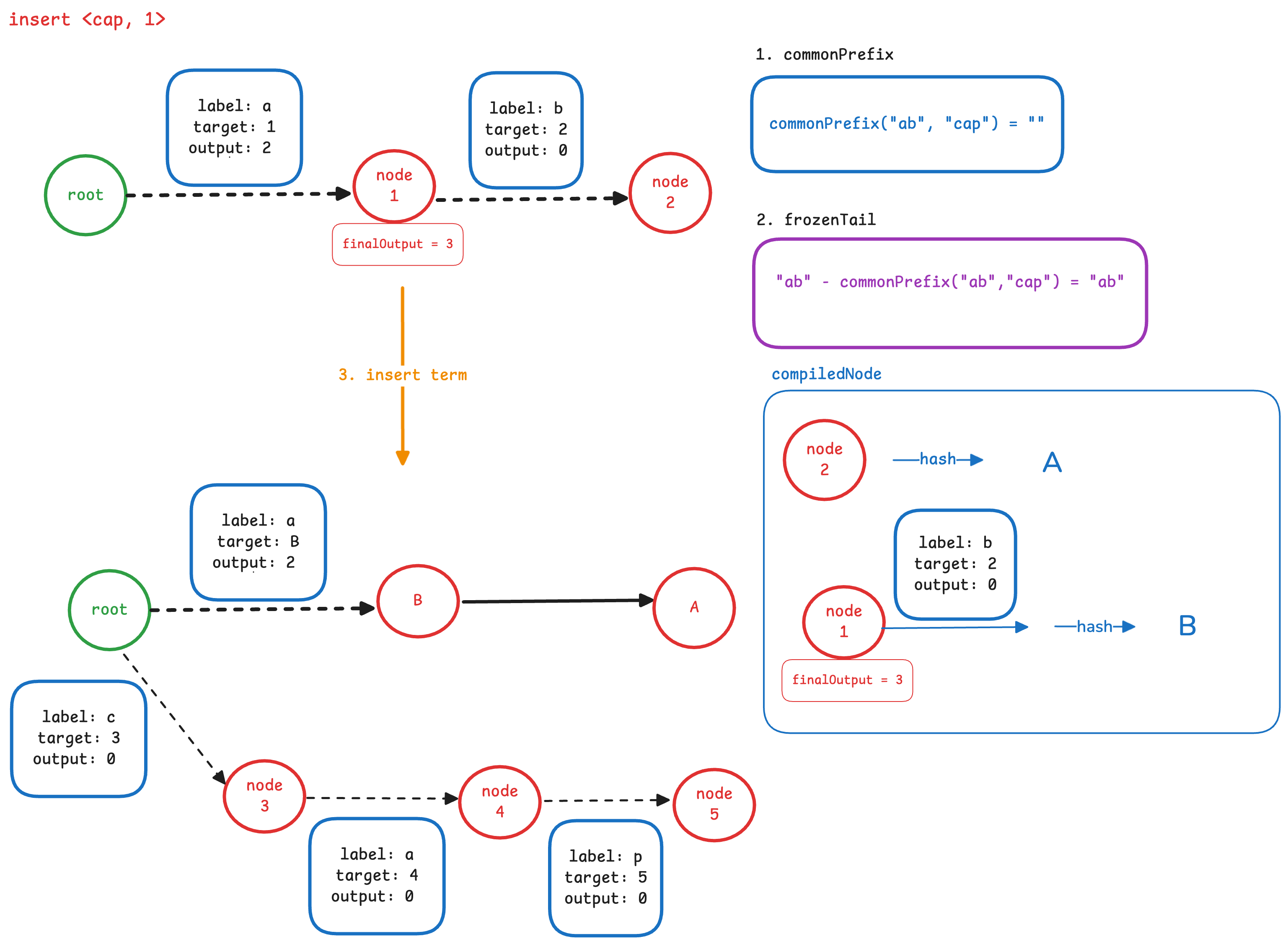
• 3.4 调整输出

这个例子中，没有相同的前缀，因此只需将分叉节点（根节点）的最后一条边的 output 设置为新的 residual 即可。如下图所示:

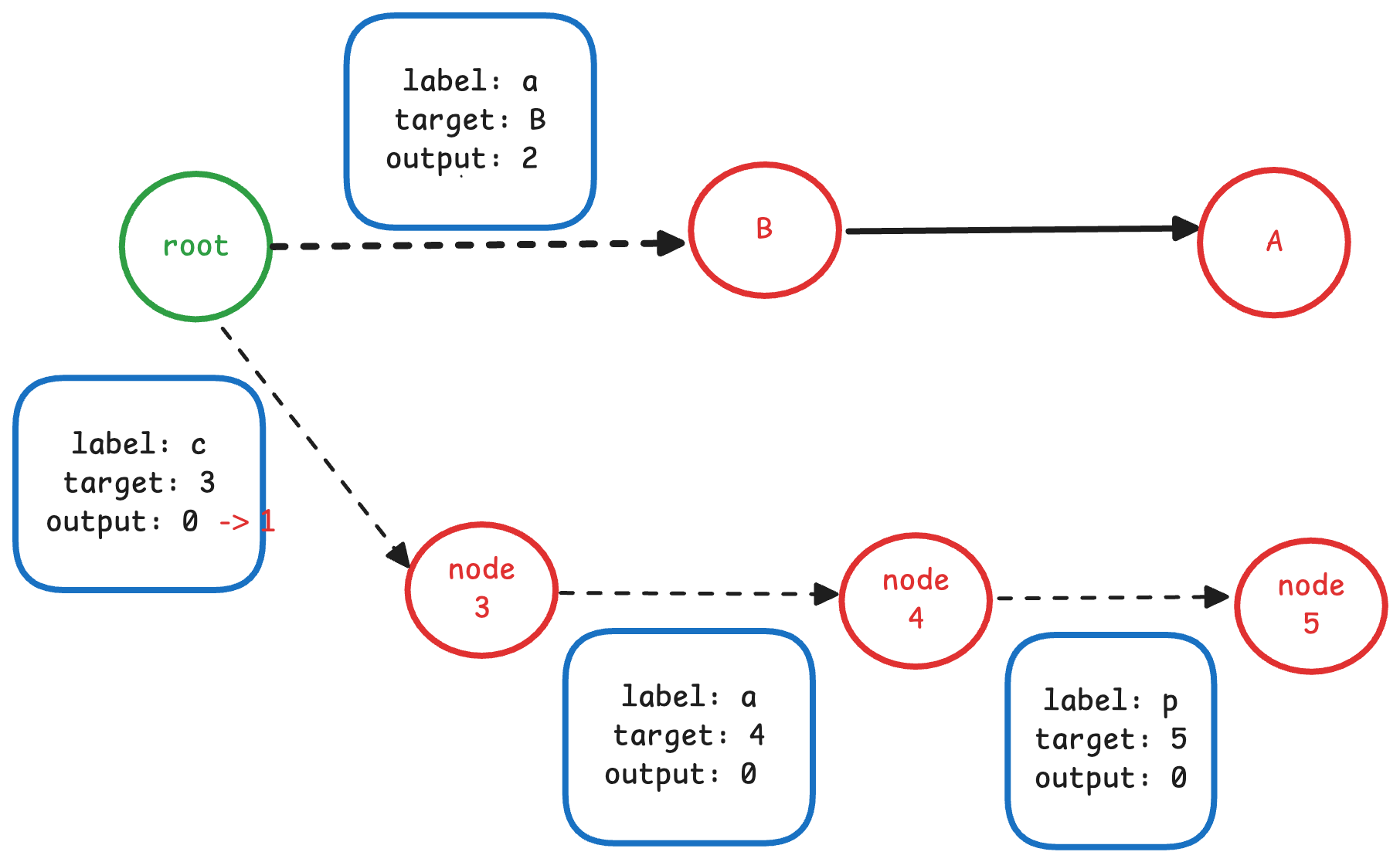
4. 插入 tap -> 1

• 4.1 寻找前缀

插入的 term 是 tap, 它与上一个term cap 共有的前缀为空。

• 4.2 处理后缀

因为共享前缀为空，因此上一个term的后缀部分为 “cap”，需要将其进行冻结 (freeze)。 冻结的过程与上一个例子类似. 这里我们发现，node 5 的信息与之前已经冻结的 node 2 一样，因此它们的 hash 值也相同，可以对该节点复用。

将 node 5 父节点（node 4）对应边的指向改为已冻结的节点(compiledNode)即可。

• 4.3 插入新的输入

我们需要插入当前term的后缀部分 “tap”。 与上一个例子类似，需要从根节点开始，依次插入三条边以及一个终止节点。

• 4.4 调整输出

仍与上一个例子一样，只需将分叉节点（根节点）最后一条边的 output 设置为新的 residual 即可。

因为这个例子与上一个例子非常类似，所以直接给出最终结果，如下图所示:

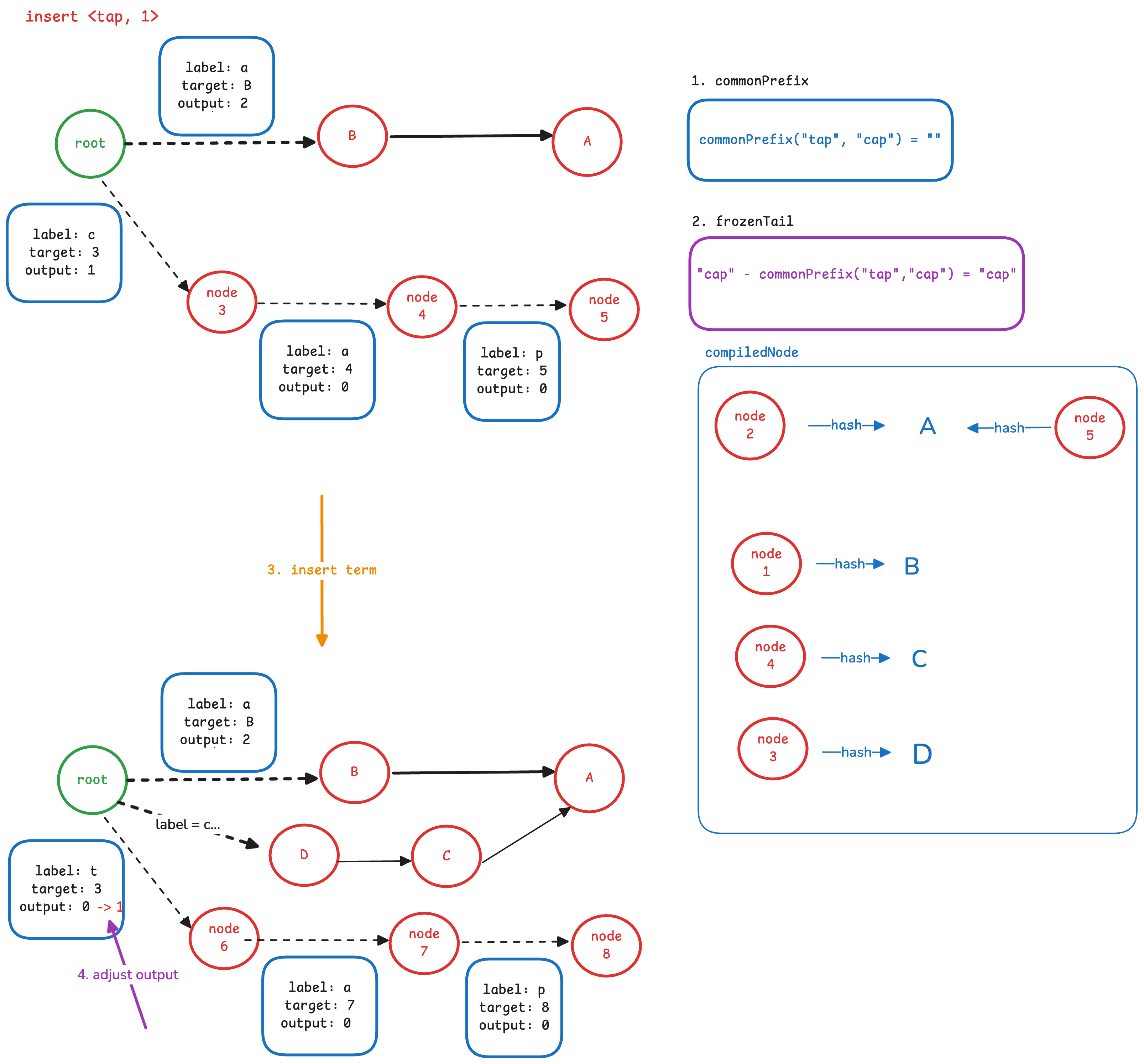
5. 冻结剩余节点

当所有 term 插入完毕，还需把剩余未冻结的节点自底向上依次冻结。在本例中，依次冻结 node 8 → node 7 → node 6 → root。过程中会不断命中等价节点并复用其地址：

首先是 node 8

这个节点什么都没有，仅仅是一个终止节点。与之前的 node 2 一样，因此可以复用node A(冻结后的node 2)。随后 让 node 7 对应边指向 node A。如下图所示:

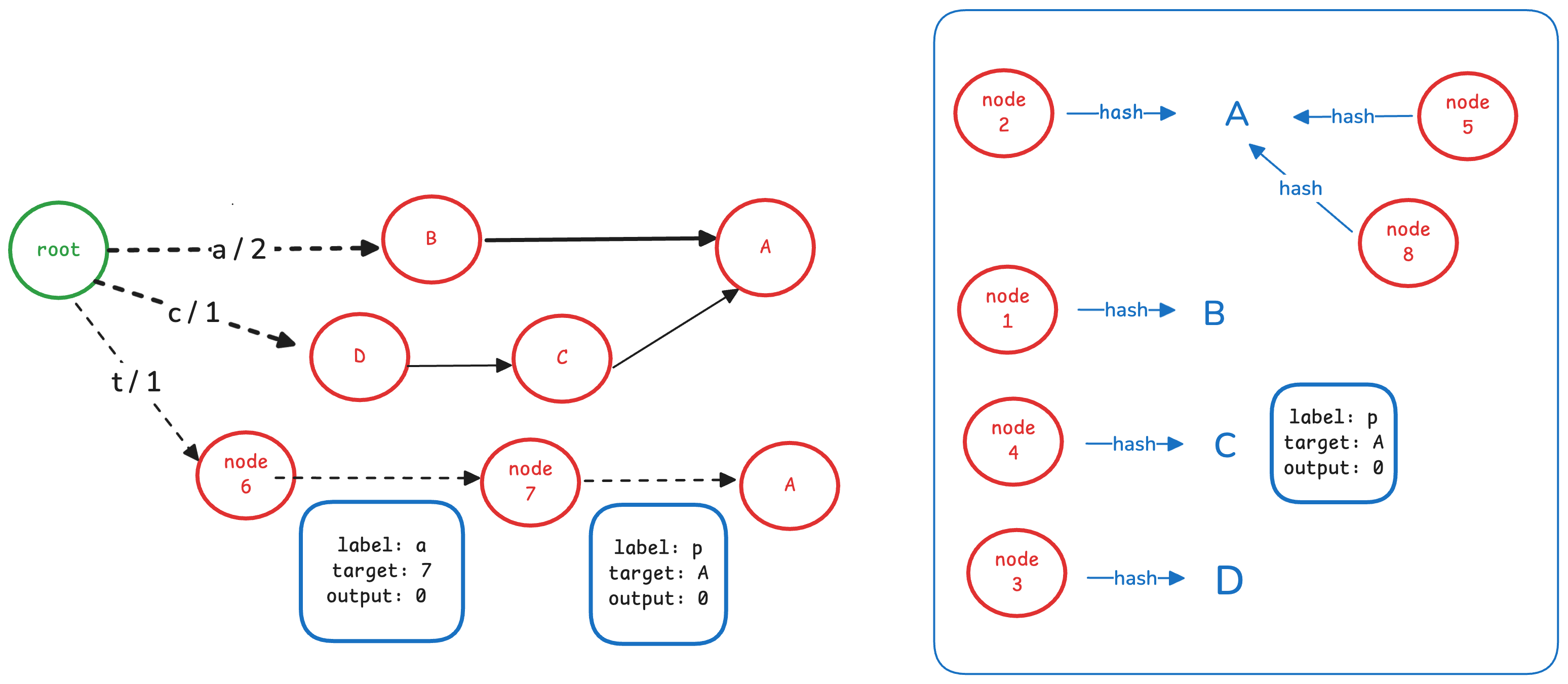
接下来是 node 7

这个节点的出边的 label 为 p, 指向node A，output 为 0。 它与已冻结的 node C 完全一样，因此可以复用node C。 让 node 6 对应边指向node C。如下图所示:

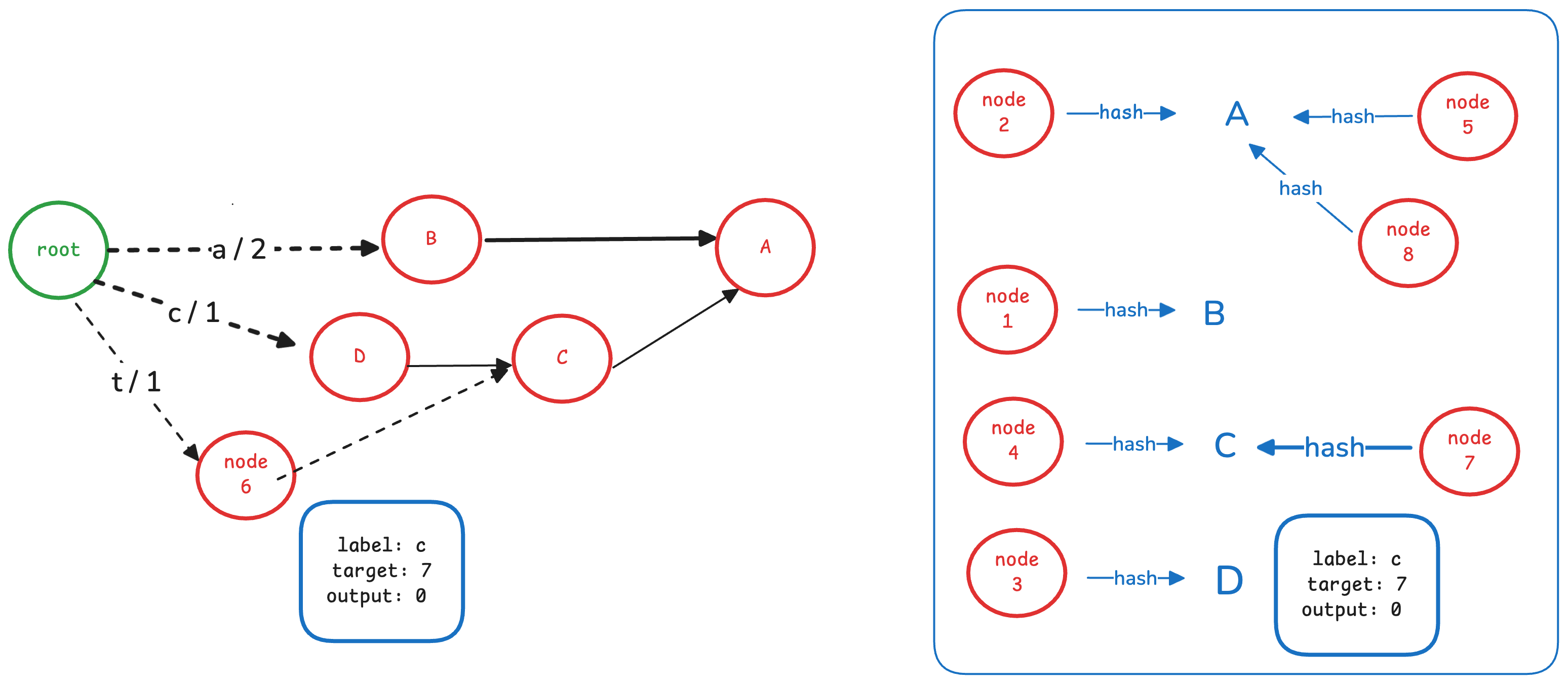
然后是 node 6

这个节点的出边的 label 为 a, 指向node C，output 为 0。 它与已冻结的 node D 一样，因此可以复用node D。 让根节点的对应边指向node D。如下图所示:

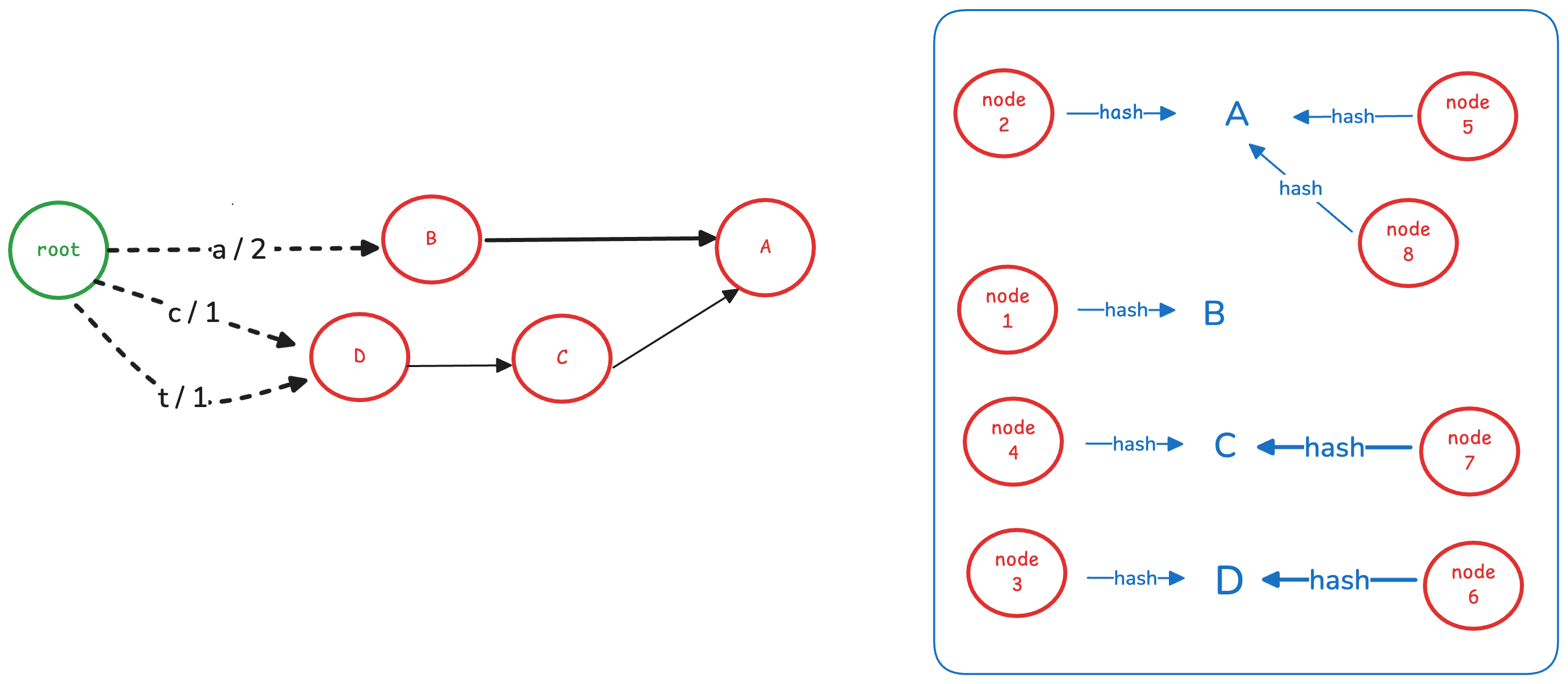
最后是根节点，因为根节点不会与其他节点重复，因此直接将其存储下来即可。

最后的FST结构如下图所示:

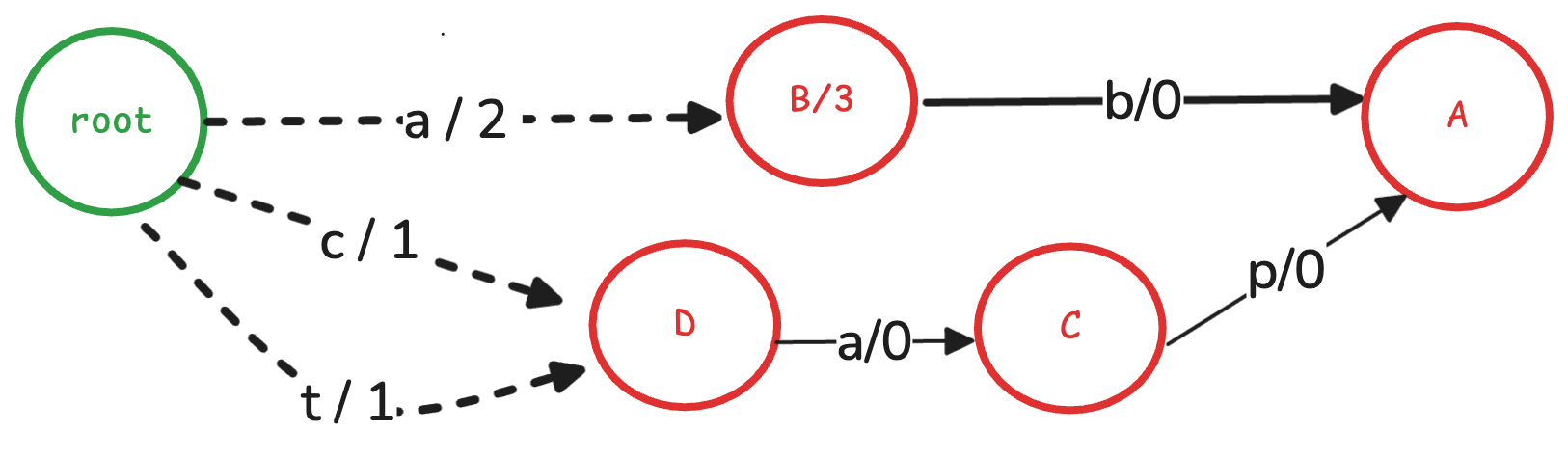
总结

本文介绍了 FST 的基本结构与查找/构建算法中的具体流程与细节。提供了一个对FST较为宏观的视角，方便读者理解 FST 的整体原理。 但是具体如何用代码将FST实现出来，本文并没有涉及。 在后续文章中，将介绍 FST 的具体实现代码，帮助读者建立起从理论到实践的完整认知。