tang-hi

Don't Panic

揭秘高维向量：巧用“反直觉”特性，让向量搜索飞起来！

Posted at # vector search # database # interesting

随着向量搜索的广泛应用，向量维度已从几十增长到上千，带来了显著的计算和存储压力。本文将探讨如何利用高维向量的特性来应对这些挑战，主要包含以下内容：

  1. 高维向量的独有特性
  2. AdSampling 算法的原理与实现
  3. RaBitQ 算法的原理与实现
  4. 总结

高维向量的独有特性

为了提升文章的可读性，本文非必要不进行数学推导，而是给读者一个感性的认识，并通过代码实验验证结论。

1. 在高维空间中，任意两个向量几乎都是正交的

如果提问我们在二维空间中，随机生成两个向量，它们之间的夹角是多少？我们可能会理所当然的认为，在[0,1800, 180]之间任意的角度都有可能。 但是当这个问题来到高维空间时，答案就不是这样了。我们可以通过下面的代码来验证这个结论。

Github Gist

从运行结果可以看到，随着维度的增加，任意两个随机向量的夹角趋近于 90∘90^\circ，即几乎正交。这说明在高维空间中，任意两个向量几乎都是垂直的。

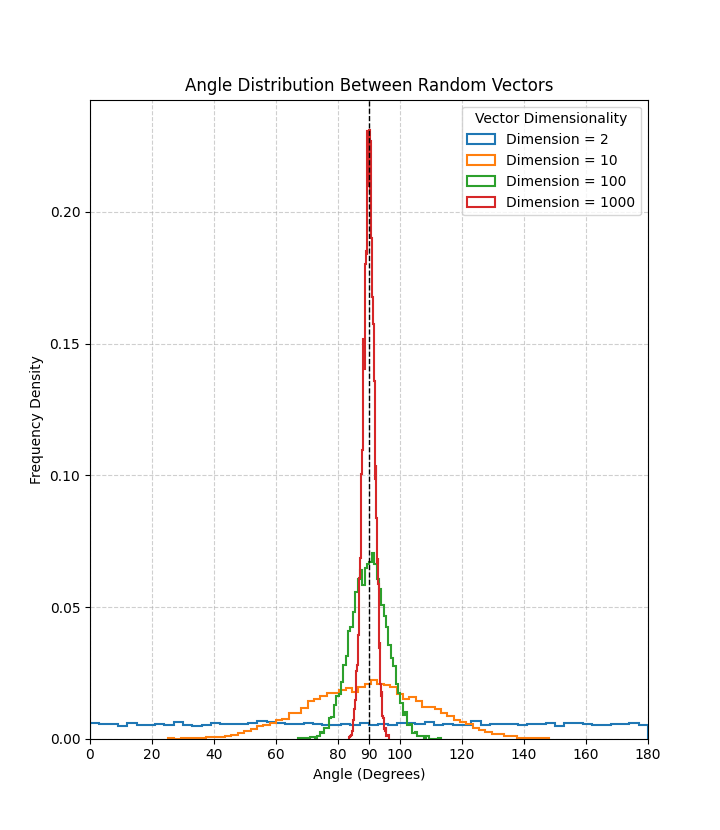
高维向量的夹角分布

详细证明可参考这里。

2. 存储 NN 个向量，只需要 O(log⁡N)\mathcal{O}(\log N) 维空间

这个特性实际上是 JL引理（Johnson-Lindenstrauss Lemma）的一个应用。JL引理 是一个非常重要的结论，它表明对高维向量进行降维时，在保持相对距离基本不变的情况下，降维后的维数只与向量的个数有关，而与原始维数无关。

也就是说，我们只需要 O(log⁡N)\mathcal{O}(\log N) 维的空间就可以存储 NN 个向量。

这个结论也回答了一个常见问题：向量的维数是否会随着业务/时间的推移而无限增加？

答案是：不会。因为我们需要处理的向量个数是有限的，所以只需要 O(log⁡N)\mathcal{O}(\log N) 维即可保证较高的召回率。

之前了解到有团队在调研如何使用软硬件结合的方式处理4096维的向量，但也许他们永远不会遇到4096维的向量。:)

有兴趣的读者可以参考这篇文章，里面详细介绍了 JL引理 的证明过程。事实上，JL引理 还有许多有用的推论，后文也会用到。

接下来介绍两篇论文，分别是 AdSampling 和 RaBitQ 算法，这两者都利用了高维向量的特性来减少计算和存储压力。

AdSampling 算法的原理与实现

在介绍 AdSampling 之前，我们先考虑一个场景。假设我们需要判断两个1024维的向量，它们的 L2距离 是否小于某个 阈值 ？通常的做法是计算每个维度的差值平方和。这意味着需要进行1024次乘法和加法运算。那么，有没有办法在未计算完所有维度的情况下，就判断出这两个向量的L2距离小于该阈值呢？答案是肯定的。

通过 JL引理（Johnson-Lindenstrauss Lemma），我们有如下公式：

P(∣Dd∥Px∥−∥x∥∣≤ϵ∥x∥)≥1−2e−c0dϵ2P\left( \left| \sqrt{\frac{D}{d}} \| P x \| - \| x \| \right| \leq \epsilon \| x \| \right) \geq 1 - 2 e^{-c_0 d \epsilon^2}

这个公式的含义是：如果我们使用一个随机的 d×Dd \times D 矩阵 PP 对向量 xx 进行投影（其中 d≤Dd \le D），那么投影后向量 PxPx 的 dd 维 L2距离与原始向量 xx 的 L2距离之间的误差可以被控制在一定范围内。

这能带来什么好处呢？ 首先，我们简述向量检索的典型步骤：给定一个候选集 SS，一个查询向量 QQ，以及一个结果集 RR。我们需要遍历 SS 中的每个向量 ss，计算其与 QQ 的距离 dis=∥Q−s∥dis = \|Q - s\|。由于结果集的大小通常限定为 KK，我们需要判断 disdis 是否小于某个阈值（即当前结果集 RR 中最大的距离）。如果小于，则将 ss 加入结果集 RR。

基于上述描述和JL引理，我们可以设计一个更高效的向量检索算法：

  1. 随机生成一个 D×DD \times D 的投影矩阵 PP。
  2. 对候选集 SS 中的每个向量 ss 进行投影，得到 s′=Pss' = Ps。
  3. 对查询向量 QQ 进行投影，得到 Q′=PQQ' = PQ。
  4. 逐步计算距离 disdis：我们不一次性计算完整的距离，而是采用分批（batch）的方式。例如，设 batch size 为 bb，每次我们仅计算 dis=∥Q′−s′∥dis = \|Q' - s'\| 的前 bb 个维度的部分距离，即 dispartial=∑i=1b(Qi′−si′)2dis_{partial} = \sum_{i=1}^b (Q'_i - s'_i)^2。如果这个部分距离已经大于设定的阈值，我们就可以提前终止对该向量的计算，直接跳过。否则，继续计算下一批维度的距离，直至计算完所有维度或提前终止。

通过这种提前终止的策略，我们可以显著减少不必要的维度计算，从而提升向量检索的效率。

AdSampling 是一个相对容易实现的算法，对现有代码改动较小（其难点主要在于数学推导，而原论文作者已完成这部分工作）。然而，需要注意的一点是，由于在计算距离时，每个 batch 都需要进行阈值判断，其单次距离计算时间可能会慢于直接使用 SIMD 指令进行全维度计算的方式。因此，若想在如图搜索算法 HNSW 中应用 AdSampling 并获得显著性能提升，更推荐直接实现论文中提出的 AKNN++ 方案，通过大量被跳过的维度计算来弥补距离计算本身的时间开销。

详细实现可参考原作者的 GitHub 仓库或我的复现代码。

RaBitQ 算法的原理与实现

首先介绍 RaBitQ，这是一种量化算法，可以将 DD 维向量压缩成 DD 个比特（对于 float 而言，相当于 32×32\times 的压缩比例），同时保证 L2 距离计算的精度误差，从而保证较高的召回率。

由于 L2 距离是无界的（取值范围为 [0,+∞)[0, +\infty)），而 RaBitQ 需要保证距离计算的精度误差，因此在构建索引时，首先需要对原始向量进行归一化，即

o:=or−c∥or−c∥o := \frac{o_r - c}{\|o_r - c\|}

其中，oro_r 是原始向量，oo 是归一化后的向量，cc 是中心向量。

1. RaBitQ 索引构建

所有向量量化都可分为两步：

  • 确定 codebook
  • 根据 codebook 对向量进行量化

1.1 确定 codebook

由于所有向量都做了归一化处理，数据点大致均匀分布在单位超球面上。因此，直观上 codebook 应具备以下特点：

  1. 均匀分布在单位超球面上
  2. 每个维度只有两个可能的取值（便于压缩为 1 个比特）

一种自然的 codebook 构造方式是：每个维度只取两个值 +1D+\frac{1}{\sqrt{D}} 和 −1D-\frac{1}{\sqrt{D}}，所有组合构成 2D2^D 个单位向量。即：

C:={(±1D,±1D,…,±1D)}C := \left\{ \left( \pm \frac{1}{\sqrt{D}}, \pm \frac{1}{\sqrt{D}}, \ldots, \pm \frac{1}{\sqrt{D}} \right) \right\}

这种构造方式保证了 codebook 均匀分布在单位超球面上，并且每个维度只有两种可能的取值。

但这种方式仍有缺陷：对某些单位向量的量化误差非常小（如 (1D,...,1D)(\frac{1}{\sqrt{D}}, ..., \frac{1}{\sqrt{D}})），但对另一些（如 (1,0,...,0)(1, 0, ..., 0)）则误差较大。

为解决此问题，可以给 codebook 加入“随机旋转”：先随机生成一个正交矩阵 PP，用 PP 对 codebook 里的每个向量做一次旋转，得到最终的 codebook：

Crand:={Px∣x∈C}C_{\text{rand}} := \{ P x \mid x \in C \}

这样，所有 codebook 向量依然是单位向量，且经过随机旋转后，原本偏向某些方向的“偏好”被消除了，所有方向都一视同仁。

1.2 根据 codebook 对向量进行量化

确定 codebook 后，对向量量化的目标是：找到与待量化向量距离最近的 codebook 向量，并用它替代原始向量。即：

arg⁡min⁡x∈C∥o−Px∥2\mathop{\arg\min}_{x \in C} \| o - P x \|^2

推导后可得：

=arg⁡max⁡x∈C⟨o,Px⟩= \mathop{\arg\max}_{x \in C} \langle o, P x \rangle

利用正交矩阵的性质，有：

⟨o,Px⟩=⟨P−1o,x⟩\langle o, P x \rangle = \langle P^{-1} o, x \rangle

其中 P−1P^{-1} 是正交矩阵 PP 的逆（等于其转置）。P−1P^{-1} 和 oo 都已知，可以直接计算。要使 ⟨o,Px⟩\langle o, P x \rangle 最大，只需找到与 P−1oP^{-1} o 每一维正负号相同的 codebook 向量即可。

因此，对向量 oo 进行量化的步骤为：

  1. 保存构建 codebook 时所用的 PP
  2. 计算 P−1oP^{-1} o
  3. 取 P−1oP^{-1} o 每一维的正负号
    • 正：该维取 +1D+\frac{1}{\sqrt{D}}
    • 负：该维取 −1D-\frac{1}{\sqrt{D}}
  4. 用 PP 对量化后的向量反变换，得到最终量化结果

这样，我们实际上只需要存储 P−1oP^{-1} o 每一维的正负号(因为每一维的绝对值都是固定的 1D\frac{1}{\sqrt{D}}，正负号决定了该维度是取 +1D+\frac{1}{\sqrt{D}} 还是 −1D-\frac{1}{\sqrt{D}})，即 DD 个比特，就可以表示原始的 DD 维浮点数向量（通常每个维度需要32个比特），实现了惊人的压缩效果.

2. RaBitQ 索引查询

量化后，可以对向量进行查询。我们需要考虑原始向量和查询向量的 L2 距离：

∥or−qr∥2=∥(or−c)−(qr−c)∥2\| o_r - q_r \|^2 = \| (o_r - c) - (q_r - c) \|^2 =∥or−c∥2+∥qr−c∥2−2⋅∥or−c∥⋅∥qr−c∥⋅⟨q,o⟩= \| o_r - c \|^2 + \| q_r - c \|^2 - 2 \cdot \| o_r - c \| \cdot \| q_r - c \| \cdot \langle q, o \rangle

其中 oro_r 和 qrq_r 分别是原始和查询向量，cc 是中心向量。∥or−c∥\| o_r - c \| 可在索引构建时计算，∥qr−c∥\| q_r - c \| 在查询时仅需计算一次。因此，只需计算 ⟨q,o⟩\langle q, o \rangle。

现在有了量化后的向量 oˉ\bar{o} 和归一化向量 oo，如何用 ⟨oˉ,o⟩\langle \bar{o}, o \rangle 表示 ⟨q,o⟩\langle q, o \rangle？

直接给出公式(推导见附录)：

⟨oˉ,q⟩=⟨oˉ,o⟩⋅⟨o,q⟩+⟨oˉ,e1⟩⋅1−⟨o,q⟩2\langle \bar{o}, q \rangle = \langle \bar{o}, o \rangle \cdot \langle o, q \rangle + \langle \bar{o}, e_1 \rangle \cdot \sqrt{1 - \langle o, q \rangle^2}

其中 e1e_1 是垂直于 oo 的单位向量。

还记得前文提到的高维特性吗？在高维空间中，任意两个向量几乎都是正交的。oˉ\bar{o} 为经过随机旋转的向量，因此可以近似认为 oˉ\bar{o} 和 e1e_1 是两个随机向量，即 ⟨oˉ,e1⟩\langle \bar{o}, e_1 \rangle 近似为 00。

因此有：

⟨oˉ,q⟩≈⟨oˉ,o⟩⋅⟨o,q⟩\langle \bar{o}, q \rangle \approx \langle \bar{o}, o \rangle \cdot \langle o, q \rangle

这样，计算误差也有了较为确定的界限，即 ⟨oˉ,e1⟩⋅1−⟨o,q⟩2\langle \bar{o}, e_1 \rangle \cdot \sqrt{1 - \langle o, q \rangle^2}。

现在要计算 ⟨q,o⟩\langle q, o \rangle，只需计算 ⟨oˉ,o⟩\langle \bar{o}, o \rangle 和 ⟨o,q⟩\langle o, q \rangle。其中 ⟨oˉ,o⟩\langle \bar{o}, o \rangle 可在索引构建时计算好。如何高效计算 ⟨oˉ,q⟩\langle \bar{o}, q \rangle？

为方便计算，可将 oˉ\bar{o} 转为 0/1 的二进制格式，即乘以 P−1P^{-1}（内积乘以正交矩阵不改变内积值）：

⟨oˉ,q⟩=⟨Pxˉ,q⟩=⟨xˉ,P−1q⟩\langle \bar{o}, q \rangle = \langle P \bar{x}, q \rangle = \langle \bar{x}, P^{-1} q \rangle

其中 xˉ\bar{x} 是 ±1D\pm \frac{1}{\sqrt{D}}。只需对输入的查询向量做一次正交变换，得到 P−1qP^{-1} q，然后根据量化向量的正负号取对应符号，最后结果除以 D\sqrt{D} 即可。

当然，为提升效率，论文中还有许多工程优化，详细代码可参考原作者 Github 或我的复现。

3. RaBitQ 算法总结

RaBitQ 算法的核心在于利用正交矩阵的各种特性完成高维向量的压缩与查询，同时利用高维向量“几乎正交”的特性给误差确定了上下界。这两点结合，使得 RaBitQ 在高达 32×32\times 压缩率下，仍能保持 95% 以上的召回率。

本文未能覆盖 RaBitQ 的所有细节，更多内容建议读者参考原文。

总结

这两篇论文都是同一个团队所做出的工作。相较于其他论文从工程角度上出发对向量检索进行优化。 他们从数学的角度上出发，利用高维向量的特性，优化距离计算，这一最基础也是最耗时的部分，并取得了不错的效果。 这无疑给向量检索带来新的思路。尽管论文仅仅只对L2距离进行了研究，但是对于其他的距离度量，应该也是可以获得差不多的效果。

附录

推导

⟨oˉ,q⟩=⟨oˉ,o⟩⋅⟨o,q⟩+⟨oˉ,e1⟩⋅1−⟨o,q⟩2\langle \bar{o}, q \rangle = \langle \bar{o}, o \rangle \cdot \langle o, q \rangle + \langle \bar{o}, e_1 \rangle \cdot \sqrt{1 - \langle o, q \rangle^2}

我们将 qq 拆为两个单位向量 oo 和 e1e_1 （e1e_1 是垂直于 oo 的单位向量）的组合,即

q=ocosθ+e1sinθq = o cos\theta + e_1 sin\theta

其中的 θ\theta 表示 qq 和 oo 的夹角, 对于单位向量而言，它们之间的点积等于 cosθcos\theta 所以我们可以把上述公式写为

q=⟨q,o⟩⋅o+1−⟨q,o⟩2e1q = \langle q, o \rangle \cdot o + \sqrt{1 - \langle q, o \rangle^2} e_1

我们把上述公式代入到 ⟨oˉ,q⟩\langle \bar{o}, q \rangle 中

⟨oˉ,q⟩=⟨oˉ,⟨q,o⟩⋅o+1−⟨q,o⟩2e1⟩\langle \bar{o}, q \rangle = \langle \bar{o}, \langle q, o \rangle \cdot o + \sqrt{1 - \langle q, o \rangle^2} e_1 \rangle

根据点积的结合律，我们可以得到

⟨oˉ,q⟩=⟨oˉ,⟨q,o⟩⋅o⟩+⟨oˉ,1−⟨q,o⟩2e1⟩\langle \bar{o}, q \rangle = \langle \bar{o}, \langle q, o \rangle \cdot o \rangle + \langle \bar{o}, \sqrt{1 - \langle q, o \rangle^2} e_1 \rangle

我们再将标量提取出来, 即可完成推导

⟨oˉ,q⟩=⟨oˉ,o⟩⋅⟨o,q⟩+⟨oˉ,e1⟩⋅1−⟨o,q⟩2\langle \bar{o}, q \rangle = \langle \bar{o}, o \rangle \cdot \langle o, q \rangle + \langle \bar{o}, e_1 \rangle \cdot \sqrt{1 - \langle o, q \rangle^2}