HNSW是通过图的方式来解决向量搜索问题的算法，由Y.Malkov与D.Yashunin在论文中首次提出。

这一个Section安排如下

1. 图拥有什么样的性质可以有效的找到最近的K个向量
2. NSW(Navigable Small World)
3. HNSW(Hierarchical Navigable Small World)

1. 图的性质

我们先直观的感受一下使用图的方式来表现向量空间。

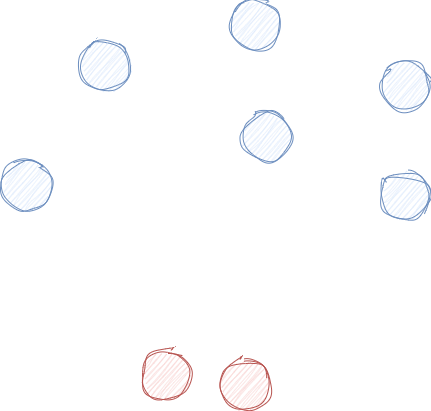
图中的点代表向量，我们可以看到，如果两个向量的距离较近，那么在图中这两个点之间的距离也会更近。当我们想要通过图的方式来解决向量搜索时，我们会希望从任一点出发可以到达图中其他所有的点，即这个图是一张联通图。

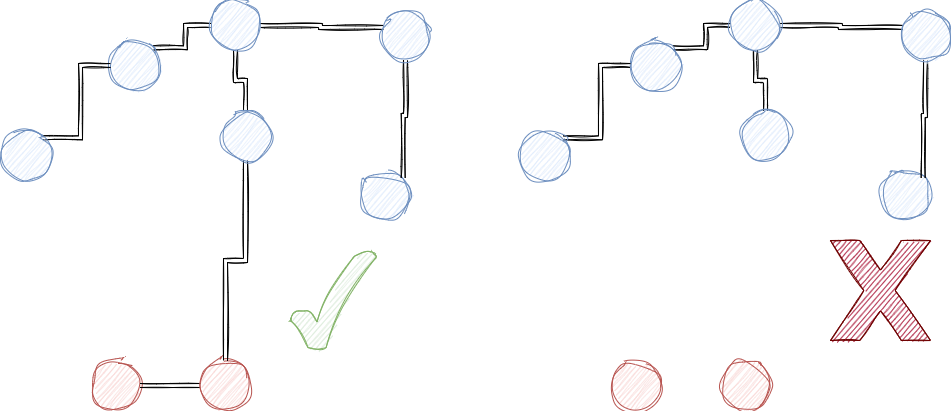
但仅仅只是联通图，仍然无法做到快速有效的找到距离最近的K个向量。考虑如下的情况，A点与B点之间相隔较远，因此如果想要从A点到达B点需要途经许多点(代表着大量的计算)，同时我们可以看到点C与许多其他的点都有连接，因此如果我们从点C开始寻找距离查询向量最近的K个点，我们会计算大量无关的点(因为与点C相连的点，其中很多大概率是与结果无关的)。

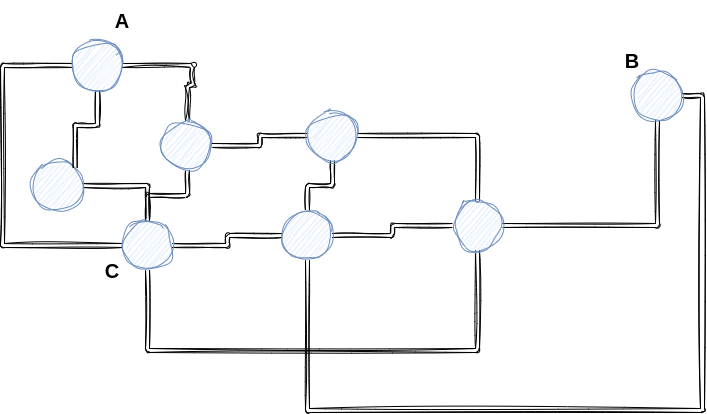
综上所述，为了可以高效而准确的找到距离查询向量最近的K个向量。我们希望构建的图有以下几个性质

1. 联通图(没有孤岛)
2. 距离较远的点,有边可以相连(long range edge)
3. 构建的图中边的数量不宜过多(大量的计算)
4. 距离相近的点，有边连接（保证召回率） 其中3,4是召回率与计算量的tradeoff。

2. NSW

NSW通过有效且简单的算法构建出满足上述要求的图，下面分别从构建以及查询两个方面来介绍NSW算法。

1. 构建

首先我们将通过随机的方式，将向量一个一个添加到图中，每一个新添加的点都会与当前图中距离该点最近的M个点相连。之所以通过M对相连的点的数量进行限制，是为了防止连接的边过多，从而影响查询效率。

我们通过一个例子来描述构建的过程，假设我们将M设置为3，并且已经将待加入的向量随机打乱。

首先，添加点A，因为当前图中没有其他任何的点，所以我们只需要添加A，而不用作任何其他的操作。后面我们继续添加点B，此时图中只有点A，点的个数小于3,因此我们可以直接将两者相连。

类似的我们向图中加入点C，点D，我们会获得以下的图

随后我们继续添加点E，此时我们会找到当前图中距离点E最近的M个点，即A，B，C并将其相互连接。

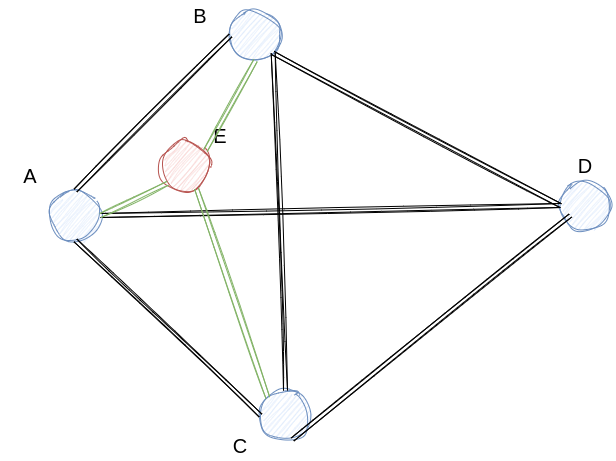
用相同的方式，我们继续添加点F，G，H，最终得到的图如下所示。

我们逐个检查NSW图是否满足我们之前要求的性质

1. 联通图，显而易见这是一张联通图
2. 距离较远的点有边可以相连，我们可以发现因为随机添加，最开始认为距离较近的点，比如A，D，随着添加的点越来越多，A，D相连的这条边成为了一条long range边。
3. 构建的图中，边的数量不宜过多。这一条因为我们始终用M控制边的数量，所以也可以满足
4. 距离较近的点，有边连接。因为我们始终与距离最近的M条边相连，因此也满足了该要求。

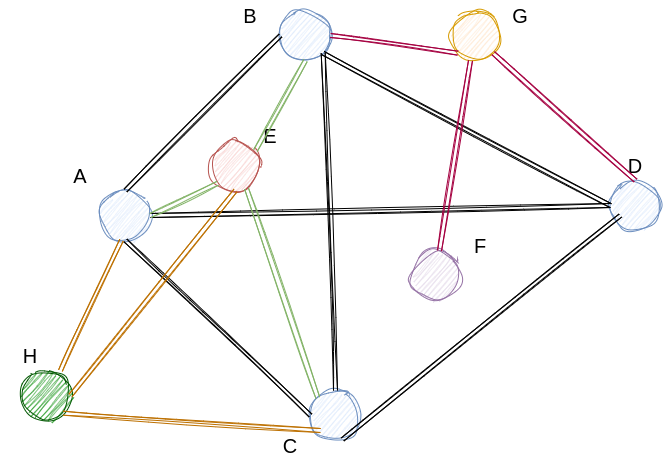
因此，我们只需要随机添加向量，并且在随机添加的过程中，与当前最近的M个点相连，我们就可以构建出一幅可以高效的进行ANN查询的图。下面我们讨论搜索的过程。

2. 搜索

因为我们通过NSW构建出的图,具有良好的特性,因此我们只需要使用简单的贪心算法就可以获得较好的搜索结果。在给定了一个query point后

1. 我们在图中随机的选择一个点作为出发点(entry point)

2. 我们计算每一个与该点相连的点，选出最近的一个点。

   a. 若该点即为entry point,搜索结束,返回entry point。

   b. 若该点不为entry point, 设置该点为entry point, 重复过程2

下图为搜索的示意图,我们可以看到因为有long range，这一高速通道的存在，我们可以快速搜索到结果。

3.HNSW

尽管NSW已经可以很好的为我们解决ANN查询的问题，但其仍然有不足之处。

1. 搜索时，NSW无法区分long range与short range，从而无法先查询long range再查询short range。
2. 当数据的聚类效应特别明显时，即使我们乱序加入向量，cluster之间相互连接的边仍然十分稀疏，从而搜索结果容易陷入局部最优，同时效率也会比较低下。

因此为了解决上述问题，HNSW作为NSW的改良版被提了出来。

1.构建

我们首先直观的感受HNSW图。我们可以看到hnsw相比于nsw多了层级的概念。我们从图中可以看到，level0中有全部的向量，随着层数的增加，向量的数量也相应的减少。

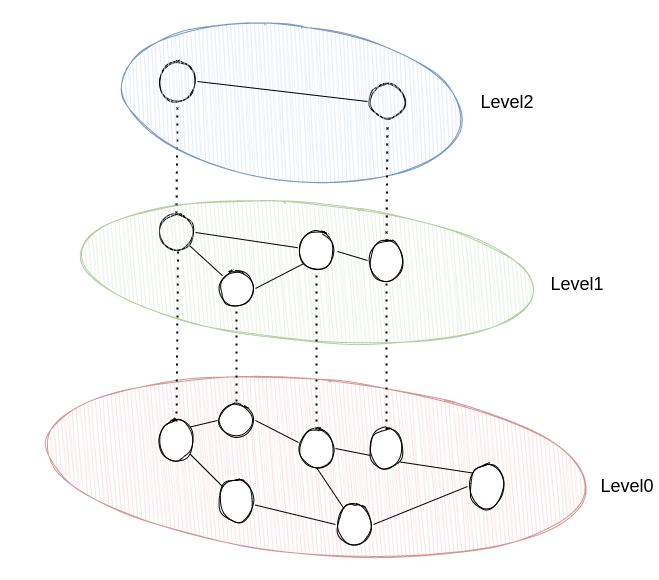
HNSW并不要求我们乱序插入向量，当我们向HNSW添加新的向量时，我们首先会通过一个指数衰减的概率函数，得到这个向量所处的最大层级(如果最大层级计算出来是3,那么level3, level2,level1,level0中都含有这个向量)。

这就意味着，绝大多数的向量所处的最高层级都是level0, 同样我们也可以认为高层级是低层级的草图（抽样），因此高层级中的向量之间大概率是long range连接，低层级中的向量则是short range连接。这样子做给我们带来的好处就是搜索时，我们可以先寻找long range的边，再寻找short range的边，即先粗查再精查。从而尽可能减少搜索的次数。

当得到这个向量所处的最大层级后，我们便需要将其添加到图中。假设，新增的向量为V, 这个向量所处的最大层级为I,HNSW的最高层级为J。添加向量时因为需要从最高层级J，一直走到最低层级0,我们将添加时所处的层级设置为C。添加的过程可以分为3个阶段

1. J >= C > I 这一阶段我们使用NSW的贪心算法，寻找距离最近的向量，随后在下一层级以这个点为搜索起点.
2. I >= C > 0 在这一阶段，我们不仅要找距离最近的向量，我们还需要将V存放到这一级的图中。我们仍旧使用贪心算法寻找距离最近的向量，不同之处在于我们会维护一个动态的列表，保存距离V最近的efCounstruction个向量，efConstruction为可调节的参数。当我们在这一层搜索完成后，我们会将这一动态列表作为Candidate,并从中取出M个向量，与其连接。
3. I = 0 这一阶段，我们采用和第二阶段一样的策略，不同的是在level0,向量V可以与最多2M个向量进行连接。

下图为一个简单的示例，新增向量所处的最高层级为1。我们首先在level2中，寻找与其最近的点(黄色标示)，找到后，我们以这个点为起点在level1中寻找与其最近的efCounstruction个点，随后与其中的M个向量进行连接。最后当我们到达level0时，我们用上一层连接的M个向量作为起点寻找符合要求的2M个向量，并与其相连。

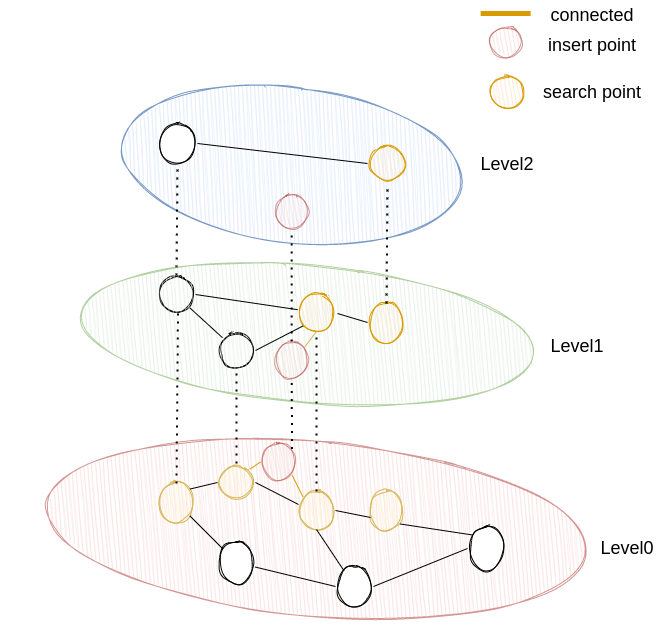
当我们在某一层中(I >= C >= 0)找到距离V最近的efConstruction向量后，我们需要从中挑选出M个向量用以与V连接。 一种简单的做法是直接从efCounstruction中挑选出最近的M个向量，但是这种做法当数据的聚类效果特别明显时，会导致不同cluster之间的连接十分稀疏，导致搜索陷入局部最优，并且查询效率降低。

因此我们采用启发式的搜索方式，假定我们新增的向量为V，挑选出的efConstruction个向量为Candidate,当前我们已经选择出需要连接的向量为Result,启发式的算法为

while len(Candidate) > 0 and len(Result) < M:
    c = pop nearest element from Candidate to V
    for r in Result:
        lowest = min(lowest, distance(r, c))
    if dis(c, V) < lowest:
        Result += c

用一张图来描述这种情况,我们从C1,C2中决定哪个点应该作为下一个连接点时，我们会选择与inserted之间的距离相比与其他result更近的点，而不是距离inserted更近的点。 按照论文中的说法，这可以帮助我们在高度聚类的数据中，取得更好的搜索效果以及效率。

The heuristic enhances the diversity of a vertex’s neighborhood and leads to better search efficiency for the case of highly clustered data.

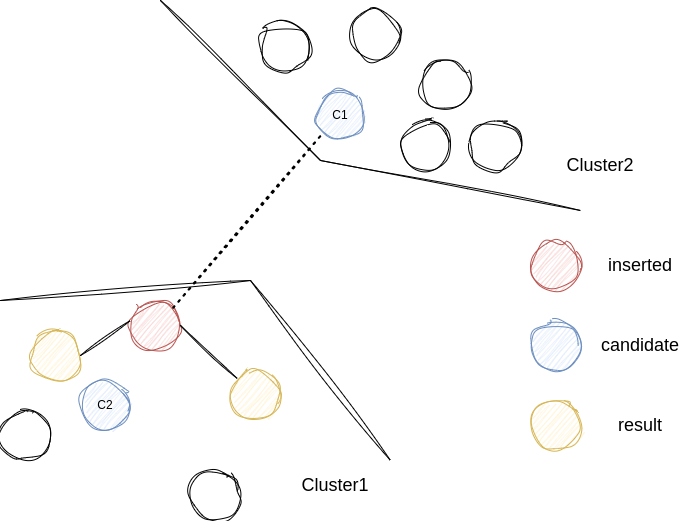
2.搜索

搜索的过程分为两个阶段

1. J >= C > 0 这一阶段我们使用NSW的贪心算法，在这一层中寻找距离最近的向量，随后在下一层级以这个点为搜索起点继续搜索.
2. I = 0 这一阶段，我们仍旧使用贪心的搜索策略，不同之处在于，我们会维护一个距离最近的efSearch个向量，并最终返回结果。

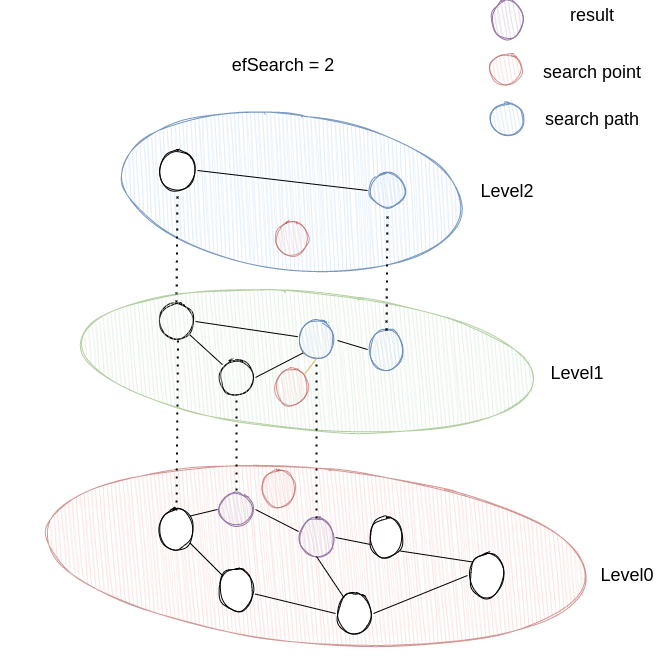
3.Summary

HNSW,通过引入层级的概念以及启发式搜索，解决了搜索时，NSW无法区分long range与short range，以及面对高度聚集的数据时，搜索效率的低下。